# Fit a LOESS model
loess_model <- loess(mpg ~ wt, data = mtcars)Introduction
If you’ve ever found yourself grappling with noisy data and yearning for a smoother representation, LOESS regression might be the enchanting solution you’re seeking. In this blog post, we’ll unravel the mysteries of LOESS regression using the power of R, and walk through a practical example using the iconic mtcars dataset.
What is LOESS Regression?
LOESS, which stands for LOcal regrESSion, is a versatile and powerful technique for fitting a curve to a set of data points. Unlike traditional linear regression, LOESS adapts to the local behavior of the data, making it perfect for capturing intricate patterns in noisy datasets.
Getting Started: Loading the mtcars Dataset
Let’s kick off our journey by loading the mtcars dataset. This dataset, featuring various car specifications, will serve as our canvas for the LOESS magic.
# Load the mtcars dataset
data(mtcars)Understanding LOESS: The Basics
Now, let’s delve into the heart of LOESS regression. In R, the magic happens with the loess() function. This function fits a smooth curve through your data, adjusting to the local characteristics.
Congratulations, you’ve just cast the LOESS spell on the fuel efficiency and weight relationship of these iconic cars!
Visualizing the Enchantment
What good is magic if you can’t see it? Let’s visualize the results with a compelling plot.
# Generate predictions from the LOESS model
predictions <- predict(loess_model, newdata = mtcars)
predictions <- cbind(mtcars, predictions)
predictions <- predictions[order(predictions$wt), ]
# Create a scatter plot of the original data
plot(
predictions$wt,
predictions$mpg,
col = "blue",
main = "LOESS Regression: Unveiling the Magic with mtcars",
xlab = "Weight (1000 lbs)",
ylab = "Miles Per Gallon"
)
# Add the LOESS curve to the plot
lines(predictions$predictions, col = "red", lwd = 2)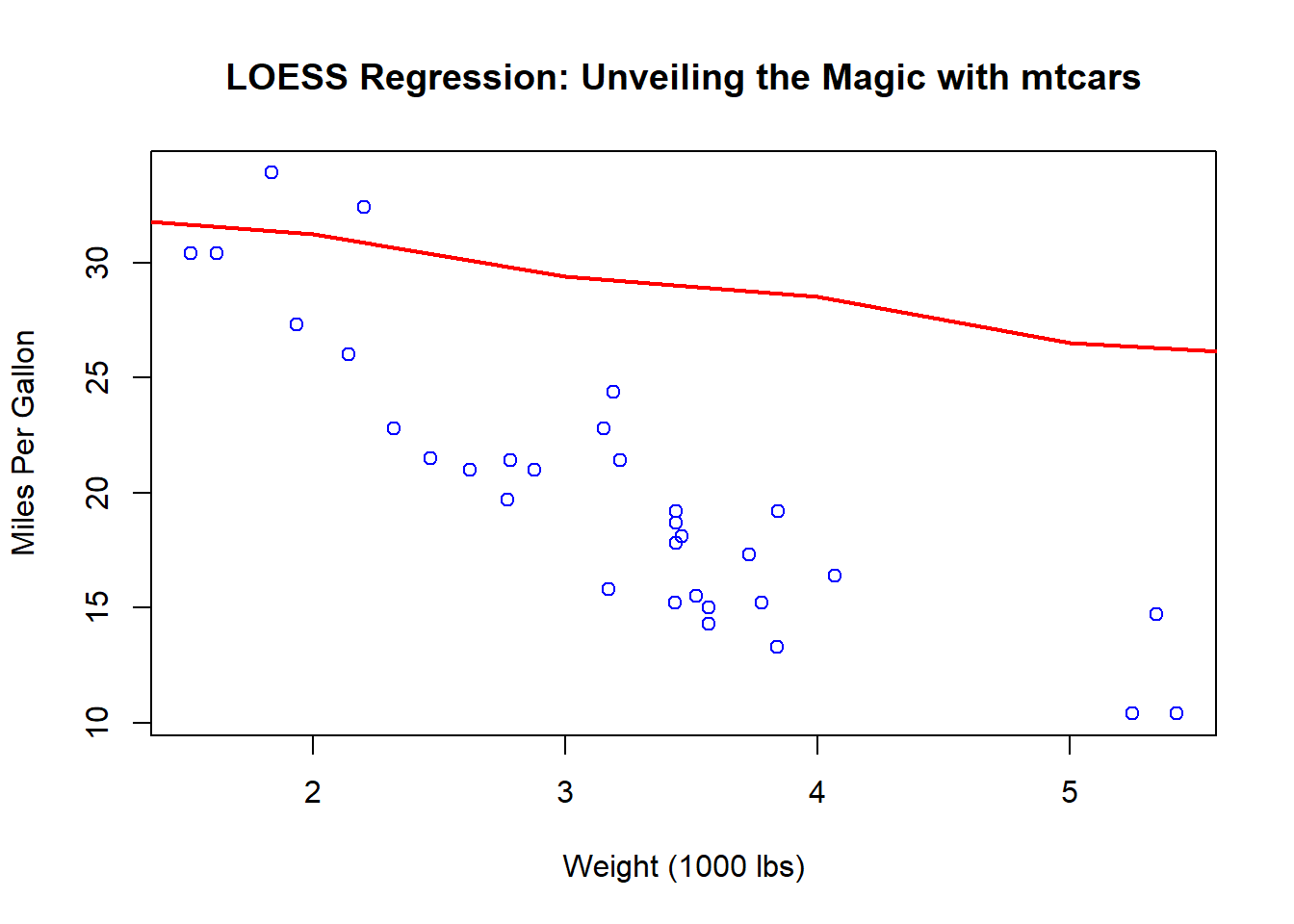
Behold, as the red curve gracefully dances through the blue points, smoothing out the rough edges and revealing the underlying trends in the relationship between weight and fuel efficiency.
Now, we did not specify any parameters for the loess() function, so it used the default values. Let’s take a look at the default parameters.
loess(formula, data, weights, subset, na.action, model = FALSE,
span = 0.75, enp.target, degree = 2,
parametric = FALSE, drop.square = FALSE, normalize = TRUE,
family = c("gaussian", "symmetric"),
method = c("loess", "model.frame"),
control = loess.control(...), ...)If you want to see the documentation in R you can use ?loess or help(loess). I have it here for you anyways but it is good to know how to check it on the fly:
Arguments formula - a formula specifying the numeric response and one to four numeric predictors (best specified via an interaction, but can also be specified additively). Will be coerced to a formula if necessary.
data - an optional data frame, list or environment (or object coercible by as.data.frame to a data frame) containing the variables in the model. If not found in data, the variables are taken from environment(formula), typically the environment from which loess is called.
weights - optional weights for each case.
subset - an optional specification of a subset of the data to be used.
na.action - the action to be taken with missing values in the response or predictors. The default is given by getOption(“na.action”).
model - should the model frame be returned?
span - the parameter α which controls the degree of smoothing.
enp.target - an alternative way to specify span, as the approximate equivalent number of parameters to be used.
degree - the degree of the polynomials to be used, normally 1 or 2. (Degree 0 is also allowed, but see the ‘Note’.)
parametric - should any terms be fitted globally rather than locally? Terms can be specified by name, number or as a logical vector of the same length as the number of predictors.
drop.square - for fits with more than one predictor and degree = 2, should the quadratic term be dropped for particular predictors? Terms are specified in the same way as for parametric.
normalize - should the predictors be normalized to a common scale if there is more than one? The normalization used is to set the 10% trimmed standard deviation to one. Set to false for spatial coordinate predictors and others known to be on a common scale.
family - if “gaussian” fitting is by least-squares, and if “symmetric” a re-descending M estimator is used with Tukey’s biweight function. Can be abbreviated.
method - fit the model or just extract the model frame. Can be abbreviated.
control - control parameters: see loess.control.
... - control parameters can also be supplied directly (if control is not specified).
Now that we see we can set things like span and degree let’s try it out.
# Create the data frame
df <- data.frame(x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))
# Fit LOESS regression models
loess50 <- loess(y ~ x, data=df, span=0.5)
smooth50 <- predict(loess50)
loess75 <- loess(y ~ x, data=df, span=0.75)
smooth75 <- predict(loess75)
loess90 <- loess(y ~ x, data=df, span=0.9)
smooth90 <- predict(loess90)
loess50_degree1 <- loess(y ~ x, data=df, span=0.5, degree=1)
smooth50_degree1 <- predict(loess50_degree1)
loess50_degree2 <- loess(y ~ x, data=df, span=0.5, degree=2)
smooth50_degree2 <- predict(loess50_degree2)
# Create scatterplot with each regression line overlaid
plot(df$x, df$y, pch=19, main='Loess Regression Models')
lines(smooth50, x=df$x, col='red')
lines(smooth75, x=df$x, col='purple')
lines(smooth90, x=df$x, col='blue')
lines(smooth50_degree1, x=df$x, col='green')
lines(smooth50_degree2, x=df$x, col='orange')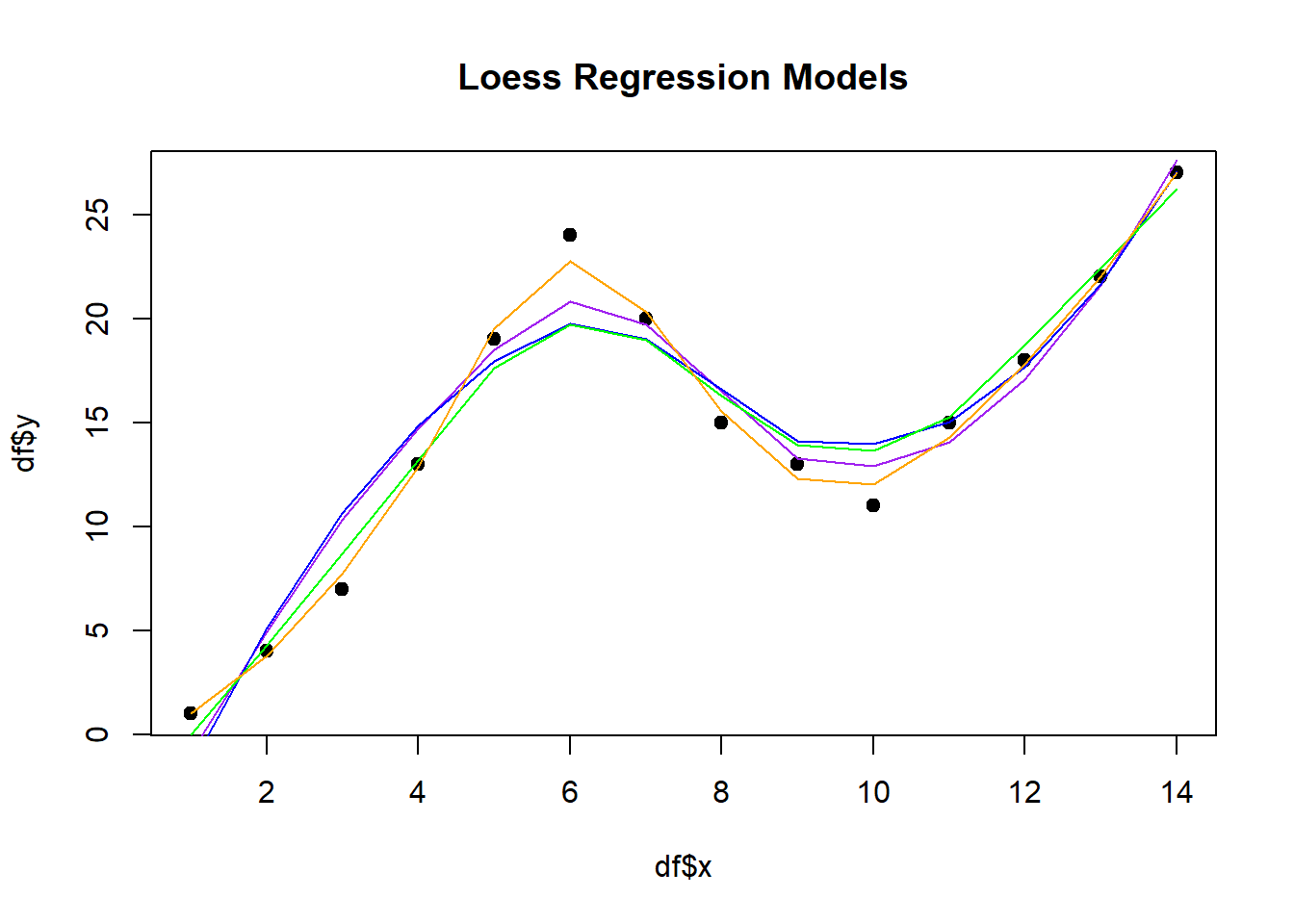
Empowering You: Try It Yourself!
Now comes the most exciting part – empowering you to wield the magic wand with the mtcars dataset or any other dataset of your choice. Encourage your readers to try the code on their own datasets, and witness the transformative power of LOESS regression.
# Your readers can replace this with their own dataset
user_data <- read.csv("user_dataset.csv")
# Fit a LOESS model on their data
user_loess_model <- loess(Y ~ X, data = user_data)
# Visualize the results
user_predictions <- predict(user_loess_model, newdata = user_data)
plot(user_data$X, user_data$Y, col = "green", main = "Your Turn: Unleash LOESS Magic", xlab = "X", ylab = "Y")
lines(user_data$X, user_predictions, col = "purple", lwd = 2)Conclusion
In this journey, we’ve walked through the fundamentals of LOESS regression in R, witnessed its magic in action using the iconic mtcars dataset, and now it’s your turn to wield the wand. As you embark on your own adventures with LOESS, remember that this enchanting technique adapts to the nuances of your data, revealing hidden patterns and smoothing the way for clearer insights.
Happy coding, and may the LOESS magic be with you! 🚗✨