Using Tidy FFT

library(healthyR.ts)
#> 
#> == Welcome to healthyR.ts ===========================================================================
#> If you find this package useful, please leave a star: 
#>    https://github.com/spsanderson/healthyR.ts'
#> 
#> If you encounter a bug or want to request an enhancement please file an issue at:
#>    https://github.com/spsanderson/healthyR.ts/issues
#> 
#> Thank you for using healthyR.ts

Introduction

In this vignette we will discuss how to use the tidy_fft function, what it does, and what it produces.

The Function

The tidy_fft function has only a few parameters, six to be exact. There are some sensible defaults made. It is important that when you use this function, that you supply it with a full time-series data set, one that has no missing data in it as this will affect your results.

Funcation and Parameters

The function and its full parameters are as follows:

tidy_fft(
  .data,
  .date_col,
  .value_col,
  .frequency = 12L,
  .harmonics = 1L,
  .upsampling = 10L
)

The .data argument is the actual formatted data that will get passed to the function, the time series data. The .date_col argument is the column that holds the datetime of interest. The .value column is the column that holds the value that is being analyzed by the function, this can be counts, averages, any type of value that is in the time series. The .frequency argument details the cyclical nature of the data, is it 12 for monthly, 7 for weekly, etc. The .harmonics argument will tell the function how many times the fft should be run internally and how many filters should be made. Finally the .upsampling argument will tell the function how much the function should up sample the time parameter.

Let us now work through a simple example.

Example

Data

Lets get started with some data.

suppressPackageStartupMessages(library(dplyr))
suppressPackageStartupMessages(library(ggplot2))
suppressPackageStartupMessages(library(timetk))

data_tbl <- AirPassengers %>%
    ts_to_tbl() %>%
    select(-index)

Now that we have our sample data, let’s check it out.

glimpse(data_tbl)
#> Rows: 144
#> Columns: 2
#> $ date_col <date> 1949-01-01, 1949-02-01, 1949-03-01, 1949-04-01, 1949-05-01, …
#> $ value    <dbl> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118, 1…

Plot Data

Lets take a look at a time series plot of the data.

suppressPackageStartupMessages(library(timetk))

data_tbl %>%
  plot_time_series(
    .date_var = date_col,
    .value    = value
  )

Now that we know what our data looks like, lets go ahead and run it through the function and assign it to a variable called output

Run Function

output <- tidy_fft(
  .data = data_tbl,
  .date_col = date_col,
  .value_col = value,
  .harmonics = 8,
  .frequency = 12,
  .upsampling = 5
)

Now that we have run the function, let’s take a look at the output.

Output

The function invisibly returns a list object, hence the need to assign it to a variable. There are a total of 4 different sections of data in the list that are returned. These are:

data
plots
parameters
model

Output Data

In this section we will go over all of the data components that are returned. We can access all of the data in the usual format output$data, which in of itself will return another list of objects, 7 to be specific. Lets go through them all.

data

The data element accessed by output$data$data is the original data with a few elements added to it. Let’s take a look:

output$data$data %>%
  glimpse()
#> Rows: 5,760
#> Columns: 6
#> $ harmonic   <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ time       <dbl> 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2,…
#> $ y_actual   <dbl> 112, NA, NA, NA, NA, 118, NA, NA, NA, NA, 132, NA, NA, NA, …
#> $ y_hat      <dbl> 292.1741, 291.0941, 290.0134, 288.9318, 287.8497, 286.7669,…
#> $ x          <dbl> 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 4, 0, 0, 0, 0,…
#> $ error_term <dbl> -180.1741, NA, NA, NA, NA, -168.7669, NA, NA, NA, NA, -149.…

error_data

The error_data element accessed by output$data$error_data is a tibble that has the original data, plus a few other elements and an error term that is the actual value minus the harmonic output. This is done for each harmonic level.

output$data$error_data %>%
  glimpse()
#> Rows: 1,152
#> Columns: 6
#> $ harmonic   <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ time       <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
#> $ y_actual   <dbl> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118,…
#> $ y_hat      <dbl> 292.1741, 286.7669, 281.3475, 275.9261, 270.5130, 265.1185,…
#> $ x          <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
#> $ error_term <dbl> -180.17406, -168.76694, -149.34751, -146.92608, -149.51298,…

input_vector

The input_vector is just the value column that was passed to the function.

output$data$input_vector
#>   [1] 112 118 132 129 121 135 148 148 136 119 104 118 115 126 141 135 125 149
#>  [19] 170 170 158 133 114 140 145 150 178 163 172 178 199 199 184 162 146 166
#>  [37] 171 180 193 181 183 218 230 242 209 191 172 194 196 196 236 235 229 243
#>  [55] 264 272 237 211 180 201 204 188 235 227 234 264 302 293 259 229 203 229
#>  [73] 242 233 267 269 270 315 364 347 312 274 237 278 284 277 317 313 318 374
#>  [91] 413 405 355 306 271 306 315 301 356 348 355 422 465 467 404 347 305 336
#> [109] 340 318 362 348 363 435 491 505 404 359 310 337 360 342 406 396 420 472
#> [127] 548 559 463 407 362 405 417 391 419 461 472 535 622 606 508 461 390 432

maximum_harmonic_tbl

The maximum_harmonic_tbl is a tibble that has data regarding the maximum harmonic entered into the function, this will be the most flexible data returned.

output$data$maximum_harmonic_tbl %>%
  glimpse()
#> Rows: 720
#> Columns: 6
#> $ harmonic   <fct> 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8,…
#> $ time       <dbl> 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2,…
#> $ y_actual   <dbl> 112, NA, NA, NA, NA, 118, NA, NA, NA, NA, 132, NA, NA, NA, …
#> $ y_hat      <dbl> 288.7745, 279.8566, 270.9787, 262.1584, 253.4132, 244.7606,…
#> $ x          <dbl> 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 4, 0, 0, 0, 0,…
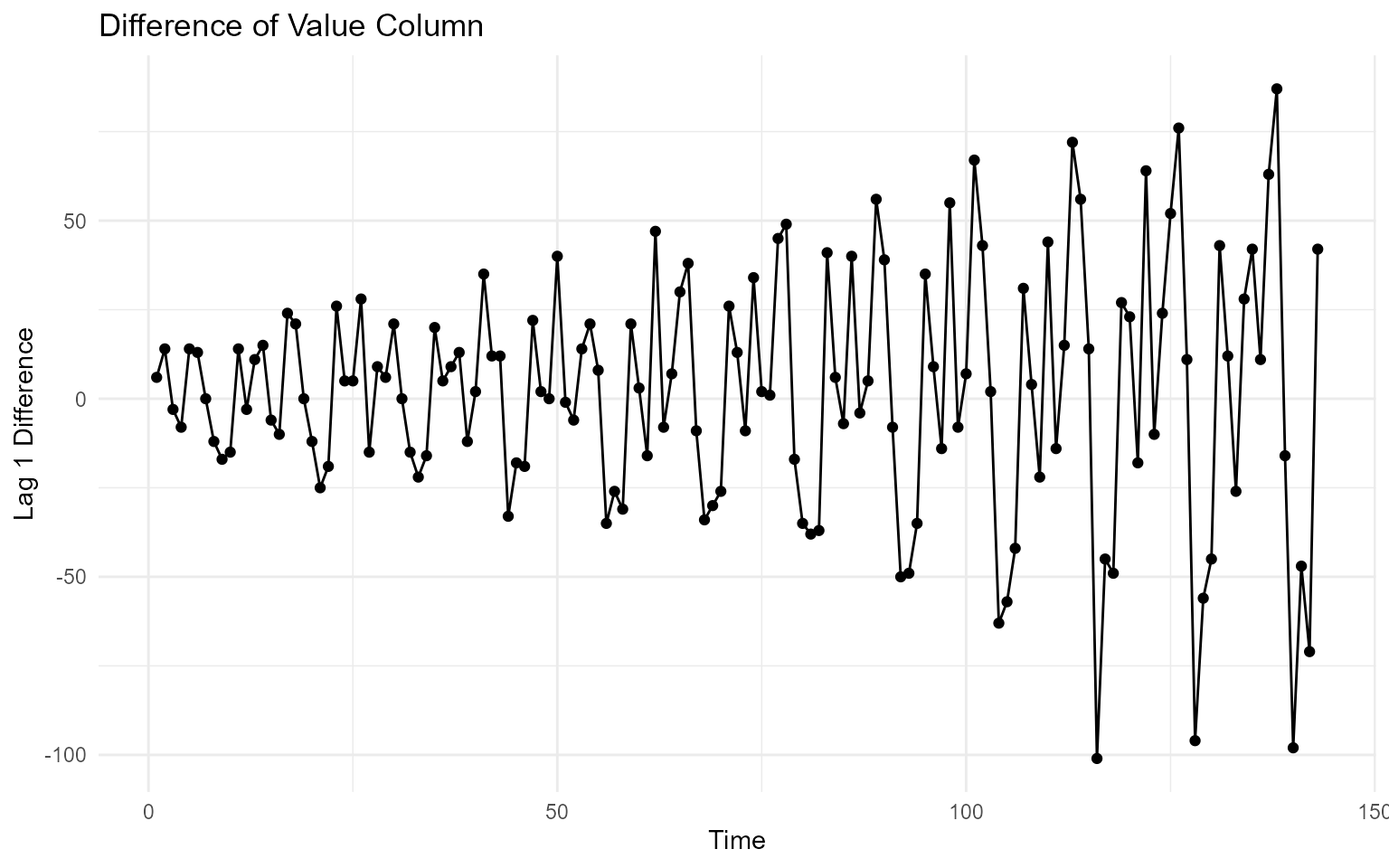
#> $ error_term <dbl> -176.77449, NA, NA, NA, NA, -126.76057, NA, NA, NA, NA, -71…

differenced_value_tbl

The differenced_value_tbl is a tibble that has a lag 1 difference of the value column supplied.

output$data$differenced_value_tbl %>%
  glimpse()
#> Rows: 143
#> Columns: 1
#> $ value <dbl> 6, 14, -3, -8, 14, 13, 0, -12, -17, -15, 14, -3, 11, 15, -6, -10…

dff_tbl

The dff_tbl is a tibble that is returned that has the fft values, the complex, real and imaginary parts.

output$data$dff_tbl %>%
  glimpse()
#> Rows: 144
#> Columns: 3
#> $ dff_trans <cpl> 40363.0000+0.0000i, 855.0323+8906.5596i, -48.1151+4098.6967i…
#> $ real_part <dbl> 40363.00000, 855.03235, -48.11512, 517.59390, -137.07676, -2…
#> $ imag_part <dbl> 0.00000, 8906.55958, 4098.69669, 3225.75142, 2323.01117, 200…

ts_obj

The last data piece of the data section is the ts_obj. This is a ts version of the input_vector

output$data$ts_obj
#>      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
#> 1949 112 118 132 129 121 135 148 148 136 119 104 118
#> 1950 115 126 141 135 125 149 170 170 158 133 114 140
#> 1951 145 150 178 163 172 178 199 199 184 162 146 166
#> 1952 171 180 193 181 183 218 230 242 209 191 172 194
#> 1953 196 196 236 235 229 243 264 272 237 211 180 201
#> 1954 204 188 235 227 234 264 302 293 259 229 203 229
#> 1955 242 233 267 269 270 315 364 347 312 274 237 278
#> 1956 284 277 317 313 318 374 413 405 355 306 271 306
#> 1957 315 301 356 348 355 422 465 467 404 347 305 336
#> 1958 340 318 362 348 363 435 491 505 404 359 310 337
#> 1959 360 342 406 396 420 472 548 559 463 407 362 405
#> 1960 417 391 419 461 472 535 622 606 508 461 390 432

Output Plots

There are a total of five plots that are returned in the list. Three of them are ggplot plots and two of them are plotly::ggplotly plots.

harmonic_plt

The harmonic_plot is a ggplot plot that shows all of the harmonic waves on the same graph if you set .harmonics greater than 1.

output$plots$harmonic_plot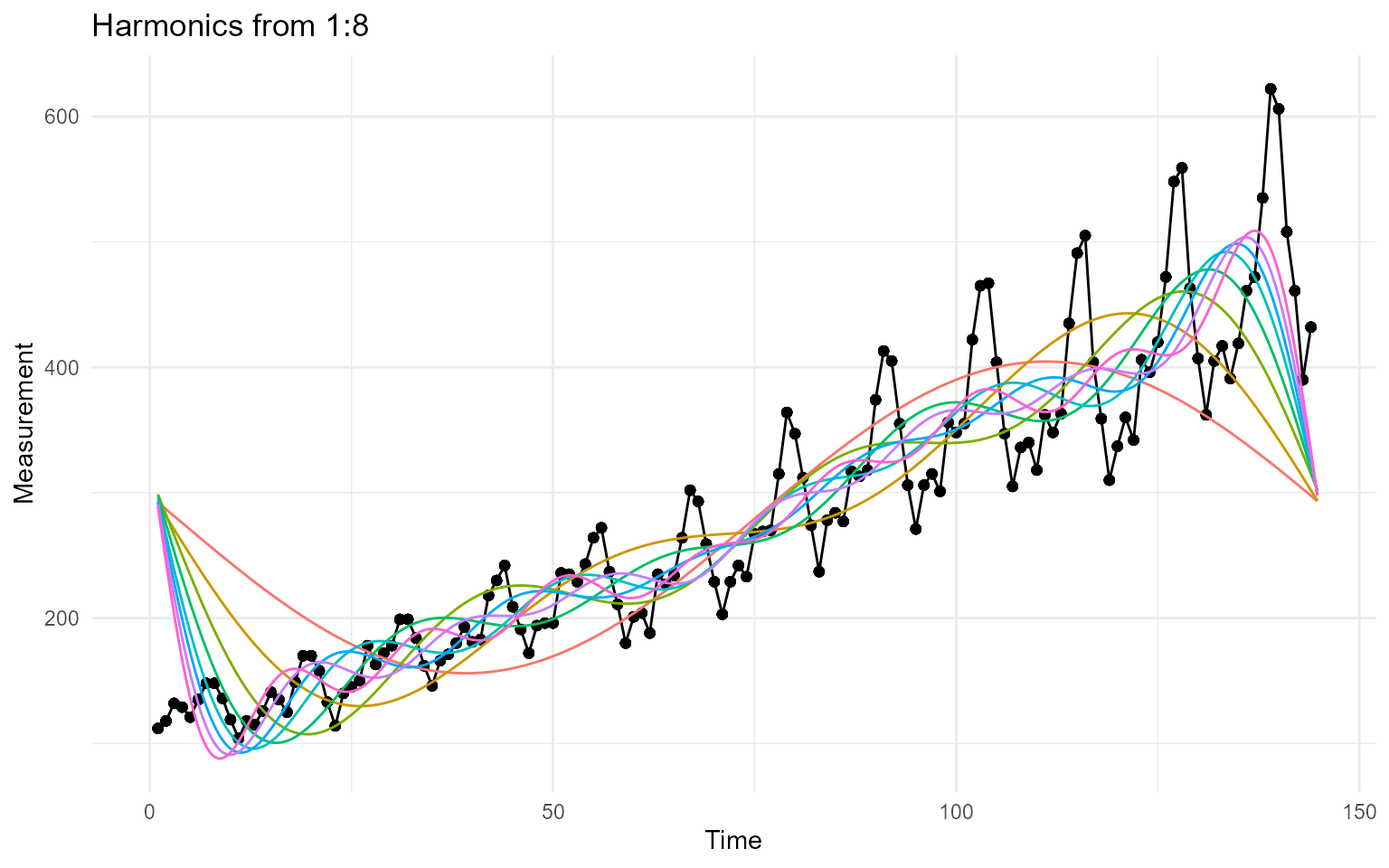

diff_plot

The diff_plot is a ggplot plot of the lag 1 differenced_value_tbl

output$plots$diff_plot

max_har_plot

The max_har_plot is a ggplot plot of the maximum harmonic wave entered into .harmonics

output$plots$max_har_plot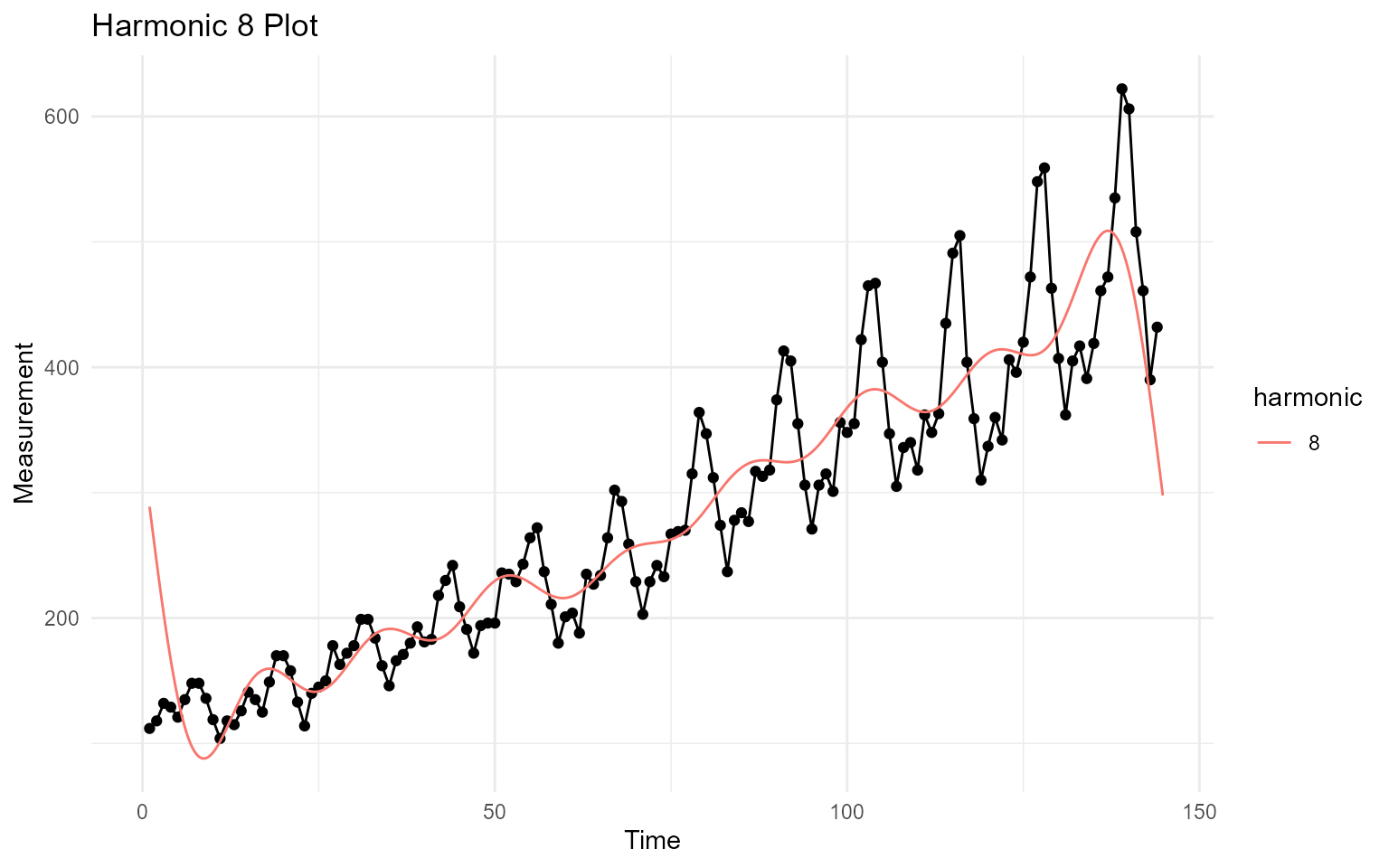

harmonic_plotly

The harmonic_plotly is a plotly::ggplotly plot of the harmonic_plot

output$plots$harmonic_plotly

max_har_plotly

The max_har_plotly is a plotly::ggplotly plot of the max_har_plot

output$plots$max_har_plotly

Output Parameters

parameters

The parameters element is a list of input parameters and internal parameters.

output$parameters
#> $harmonics
#> [1] 5
#> 
#> $upsampling
#> [1] 8
#> 
#> $start_date
#> [1] "1949-01-01 UTC"
#> 
#> $end_date
#> [1] "1960-12-01 UTC"
#> 
#> $freq
#> [1] 12

Output Model

The model portion has four pieces to it which we will look at below.

m

The parameter m is an internal parameter that is equal to .harmonics / 2. This is fed into TSA::harmonic along with the ts_obj

The parameter harmonic_obj is the object returned from TSA::harmonic

The parameter harmonic_model is the harmonic model from the TSA::harmonic

The parameter model_summary is a summary of the harmonic model.

output$model$m
#> [1] 6

output$model$harmonic_obj %>% head()
#>        cos(2*pi*t) cos(4*pi*t)   cos(6*pi*t) cos(8*pi*t)  cos(10*pi*t)
#> [1,]  1.000000e+00         1.0  1.000000e+00         1.0  1.000000e+00
#> [2,]  8.660254e-01         0.5  1.655735e-13        -0.5 -8.660254e-01
#> [3,]  5.000000e-01        -0.5 -1.000000e+00        -0.5  5.000000e-01
#> [4,]  1.157757e-12        -1.0 -5.292262e-12         1.0  3.969798e-12
#> [5,] -5.000000e-01        -0.5  1.000000e+00        -0.5 -5.000000e-01
#> [6,] -8.660254e-01         0.5  3.142992e-12        -0.5  8.660254e-01
#>      cos(12*pi*t)   sin(2*pi*t)   sin(4*pi*t)   sin(6*pi*t)   sin(8*pi*t)
#> [1,]            1 -4.134027e-13 -8.268054e-13  2.397771e-12 -1.653611e-12
#> [2,]           -1  5.000000e-01  8.660254e-01  1.000000e+00  8.660254e-01
#> [3,]            1  8.660254e-01  8.660254e-01  2.728918e-12 -8.660254e-01
#> [4,]           -1  1.000000e+00  2.315515e-12 -1.000000e+00 -4.631030e-12
#> [5,]            1  8.660254e-01 -8.660254e-01 -5.796483e-13  8.660254e-01
#> [6,]           -1  5.000000e-01 -8.660254e-01  1.000000e+00 -8.660254e-01
#>       sin(10*pi*t)
#> [1,] -5.704992e-12
#> [2,]  5.000000e-01
#> [3,] -8.660254e-01
#> [4,]  1.000000e+00
#> [5,] -8.660254e-01
#> [6,]  5.000000e-01

output$model$harmonic_model
#> 
#> Call:
#> stats::lm(formula = ts_obj ~ har_)
#> 
#> Coefficients:
#>      (Intercept)   har_cos(2*pi*t)   har_cos(4*pi*t)   har_cos(6*pi*t)  
#>         280.2986          -48.1494           16.7639           -6.3889  
#>  har_cos(8*pi*t)  har_cos(10*pi*t)  har_cos(12*pi*t)   har_sin(2*pi*t)  
#>           1.3889           -0.2534           -1.9097           -4.4632  
#>  har_sin(4*pi*t)   har_sin(6*pi*t)   har_sin(8*pi*t)  har_sin(10*pi*t)  
#>          11.6192          -11.1250           -7.9867           -6.4118

output$model$model_summary
#> 
#> Call:
#> stats::lm(formula = ts_obj ~ har_)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -203.33  -93.48  -16.96   87.17  270.67 
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)      280.2986     9.8379  28.492  < 2e-16 ***
#> har_cos(2*pi*t)  -48.1494    13.9128  -3.461 0.000726 ***
#> har_cos(4*pi*t)   16.7639    13.9128   1.205 0.230389    
#> har_cos(6*pi*t)   -6.3889    13.9128  -0.459 0.646840    
#> har_cos(8*pi*t)    1.3889    13.9128   0.100 0.920632    
#> har_cos(10*pi*t)  -0.2534    13.9128  -0.018 0.985497    
#> har_cos(12*pi*t)  -1.9097     9.8379  -0.194 0.846381    
#> har_sin(2*pi*t)   -4.4632    13.9128  -0.321 0.748870    
#> har_sin(4*pi*t)   11.6192    13.9128   0.835 0.405148    
#> har_sin(6*pi*t)  -11.1250    13.9128  -0.800 0.425367    
#> har_sin(8*pi*t)   -7.9867    13.9128  -0.574 0.566910    
#> har_sin(10*pi*t)  -6.4118    13.9128  -0.461 0.645662    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 118.1 on 132 degrees of freedom
#> Multiple R-squared:  0.1061, Adjusted R-squared:  0.03162 
#> F-statistic: 1.424 on 11 and 132 DF,  p-value: 0.169

Analyze Time Series data with tidy_fft

Steven P. Sanderson II, MPH

2024-10-13