Discrete Distribution Generators

RandomWalker provides random walk generators based on discrete probability distributions. These are ideal for modeling count data, categorical outcomes, and processes with discrete state changes.

Common Parameters
Discrete Walk
Binomial Distribution
Geometric Distribution
Hypergeometric Distribution
Multinomial Distribution
Negative Binomial Distribution
Poisson Distribution
Wilcoxon Tests
Smirnov Distribution
Comparison Guide

Common Parameters

All discrete distribution generators share these parameters:

Parameter	Type	Description	Default
`.num_walks`	Integer	Number of walks to generate	25
`.n`	Integer	Number of steps per walk	100
`.initial_value`	Numeric	Starting value for the walk	0
`.dimensions`	Integer	Spatial dimensions (1, 2, or 3)	1

Discrete Walk

`discrete_walk()`

The fundamental discrete random walk with binary outcomes (up or down).

Function Signature:

discrete_walk(
  .num_walks = 25,
  .n = 100,
  .upper_bound = 1,
  .lower_bound = -1,
  .upper_probability = 0.5,
  .initial_value = 100,
  .dimensions = 1
)

Parameters: - .upper_bound - Maximum step size (default: 1) - .lower_bound - Minimum step size (default: -1) - .upper_probability - Probability of moving up (default: 0.5)

Properties: - Simple binary outcomes - Each step is either .upper_bound or .lower_bound - Unbiased when .upper_probability = 0.5 - Can create biased walks by adjusting probability

Use Cases: - Gambler’s ruin problem - Simple gain/loss scenarios - Teaching probability concepts - Binary decision modeling

Example:

# Unbiased walk (50/50)
discrete_walk(
  .num_walks = 10,
  .n = 100,
  .upper_probability = 0.5
) |> visualize_walks()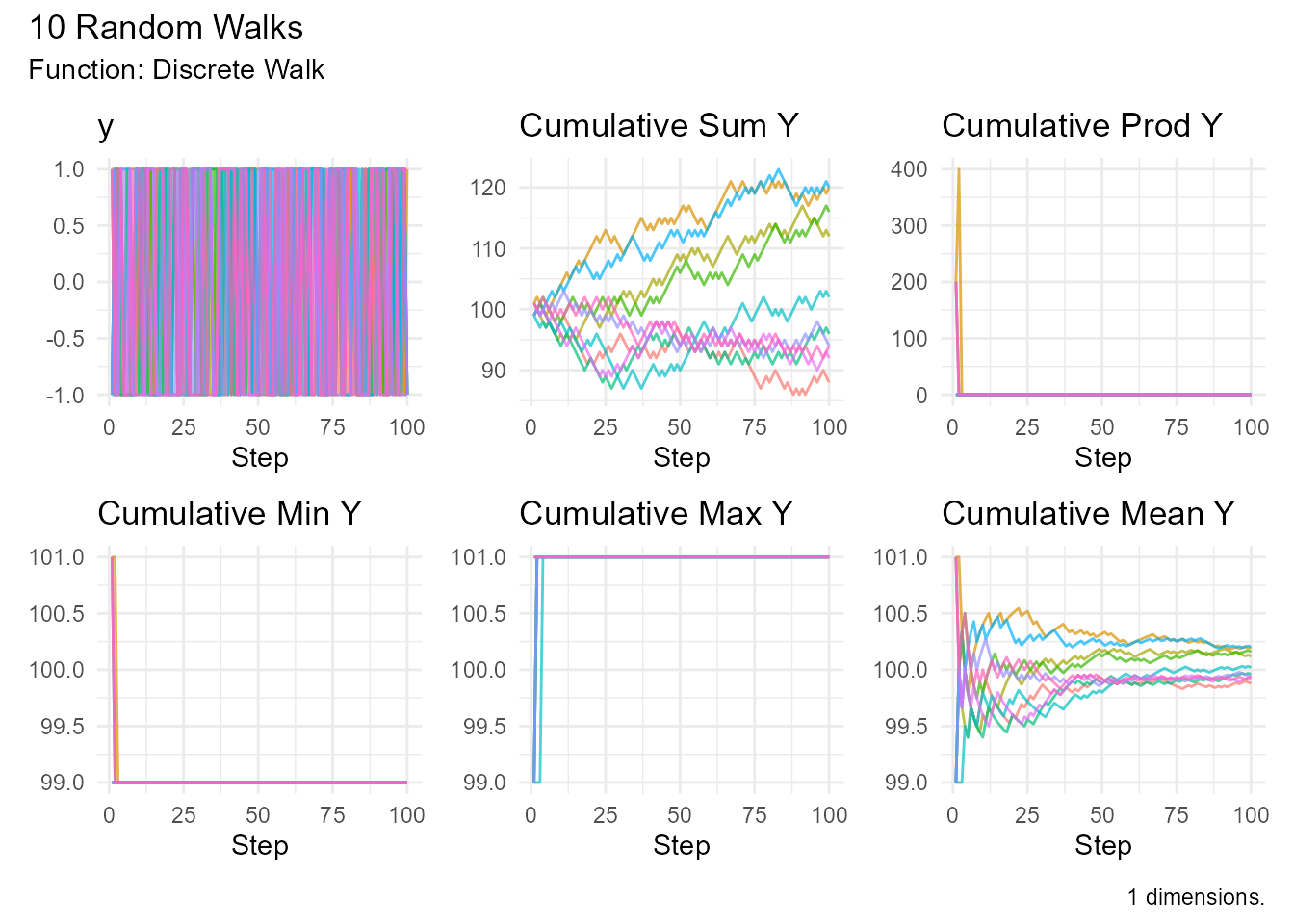

Unbiased discrete random walk showing symmetric up and down movements

# Biased upward (60% up, 40% down)
discrete_walk(
  .num_walks = 10,
  .n = 100,
  .upper_probability = 0.6
) |> visualize_walks()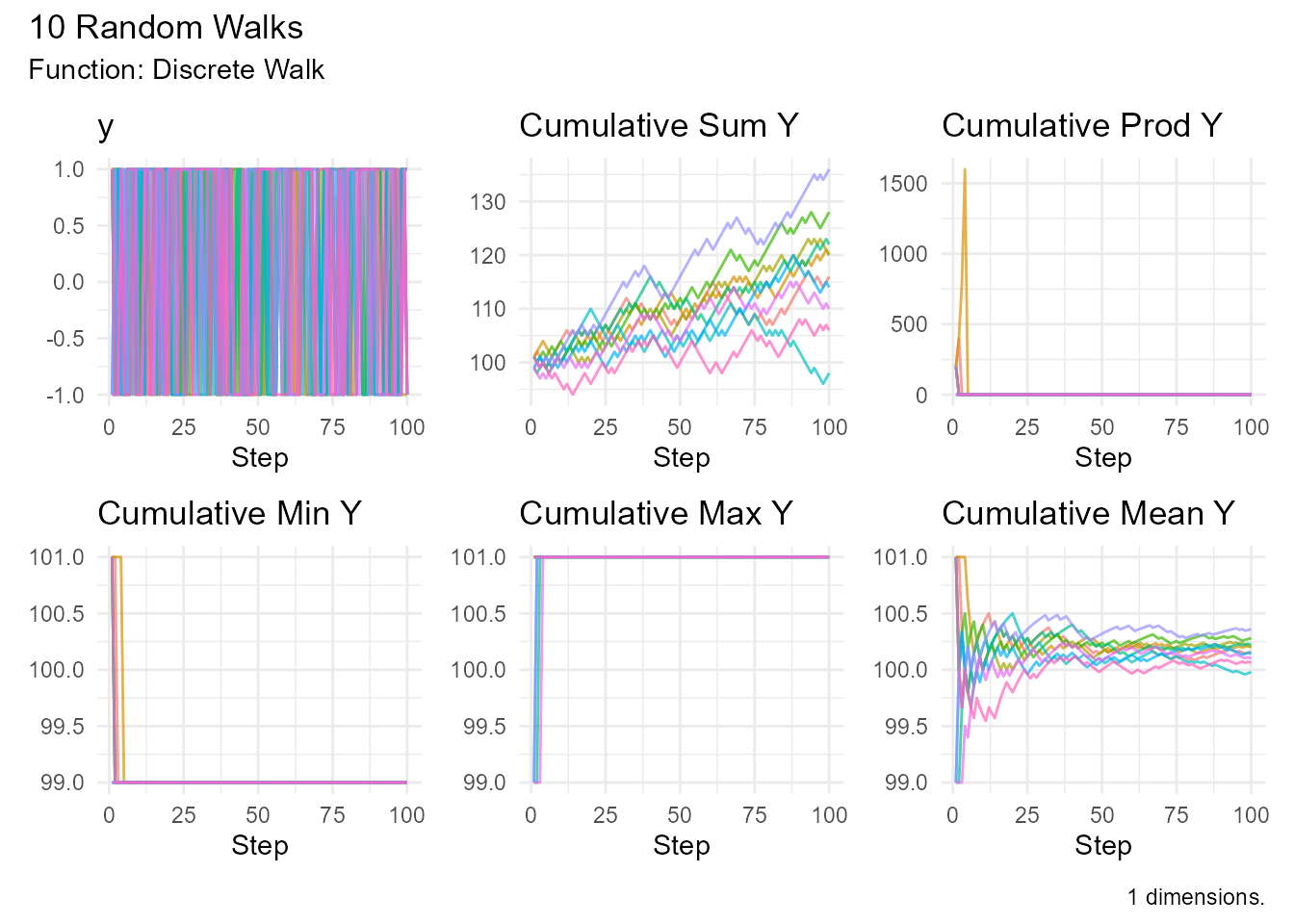

Biased discrete walk showing upward trend with 60% probability

# Gambler's ruin simulation
gambler <- discrete_walk(
  .num_walks = 100,
  .n = 1000,
  .upper_bound = 1,
  .lower_bound = -1,
  .upper_probability = 0.48,  # House edge
  .initial_value = 100
)

gambler |>
  summarize_walks(.value = cum_sum_y, .group_var = walk_number) |>
  summarize(
    prob_ruin = mean(min_val <= 0),
    avg_final = mean(max_val)
  )
#> Registered S3 method overwritten by 'quantmod':
#>   method            from
#>   as.zoo.data.frame zoo
#> Warning: There were 5 warnings in `dplyr::summarize()`.
#> The first warning was:
#> ℹ In argument: `geometric_mean = exp(mean(log(cum_sum_y)))`.
#> ℹ In group 17: `walk_number = 17`.
#> Caused by warning in `log()`:
#> ! NaNs produced
#> ℹ Run `dplyr::last_dplyr_warnings()` to see the 4 remaining warnings.
#> # A tibble: 1 × 2
#>   prob_ruin avg_final
#>       <dbl>     <dbl>
#> 1      0.05      110.

Binomial Distribution

`random_binomial_walk()`

Random walk based on binomial distribution (number of successes in n trials).

Function Signature:

random_binomial_walk(
  .num_walks = 25,
  .n = 100,
  .size = 10,
  .prob = 0.5,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .size - Number of trials per step - .prob - Probability of success in each trial

Properties: - Steps are integers: 0, 1, 2, …, size - Mean step = size × prob - Variance = size × prob × (1 - prob) - Symmetric when prob = 0.5

Use Cases: - Quality control (defects in batches) - Survey responses (yes/no questions) - Medical trials (treatment successes) - Coin flip experiments

Example:

# Fair coin flips (10 per step)
random_binomial_walk(
  .num_walks = 10,
  .size = 10,
  .prob = 0.5
) |> visualize_walks()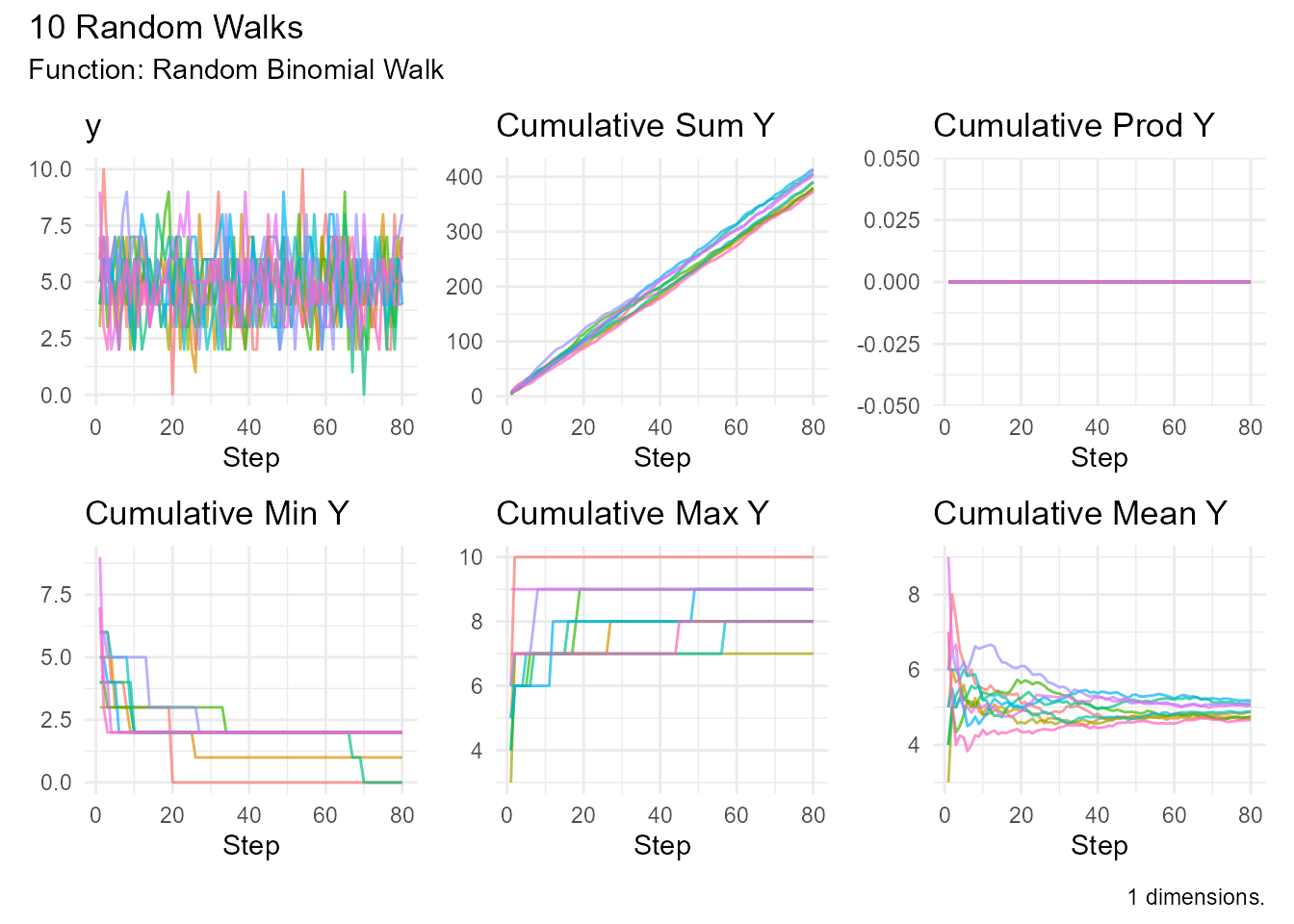

Binomial random walk with 10 coin flips per step showing symmetric behavior

# Quality control simulation
defects <- random_binomial_walk(
  .num_walks = 50,
  .n = 100,
  .size = 100,  # Batch size
  .prob = 0.05  # 5% defect rate
)

defects |>
  summarize_walks(.value = y, .group_var = walk_number) |>
  summarize(
    avg_defects_per_batch = mean(mean_val),
    max_defects = max(max_val)
  )
#> # A tibble: 1 × 2
#>   avg_defects_per_batch max_defects
#>                   <dbl>       <int>
#> 1                  5.09          12

Geometric Distribution

`random_geometric_walk()`

Random walk based on geometric distribution (number of trials until first success).

Function Signature:

random_geometric_walk(
  .num_walks = 25,
  .n = 100,
  .prob = 0.5,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .prob - Probability of success

Properties: - Steps are positive integers: 1, 2, 3, … - Memoryless property - Mean = 1 / prob - Variance = (1 - prob) / prob²

Use Cases: - Time until first success - Reliability testing - Customer conversion time - Waiting time modeling

Example:

# High probability (short waits)
random_geometric_walk(
  .num_walks = 10,
  .prob = 0.8
) |> visualize_walks()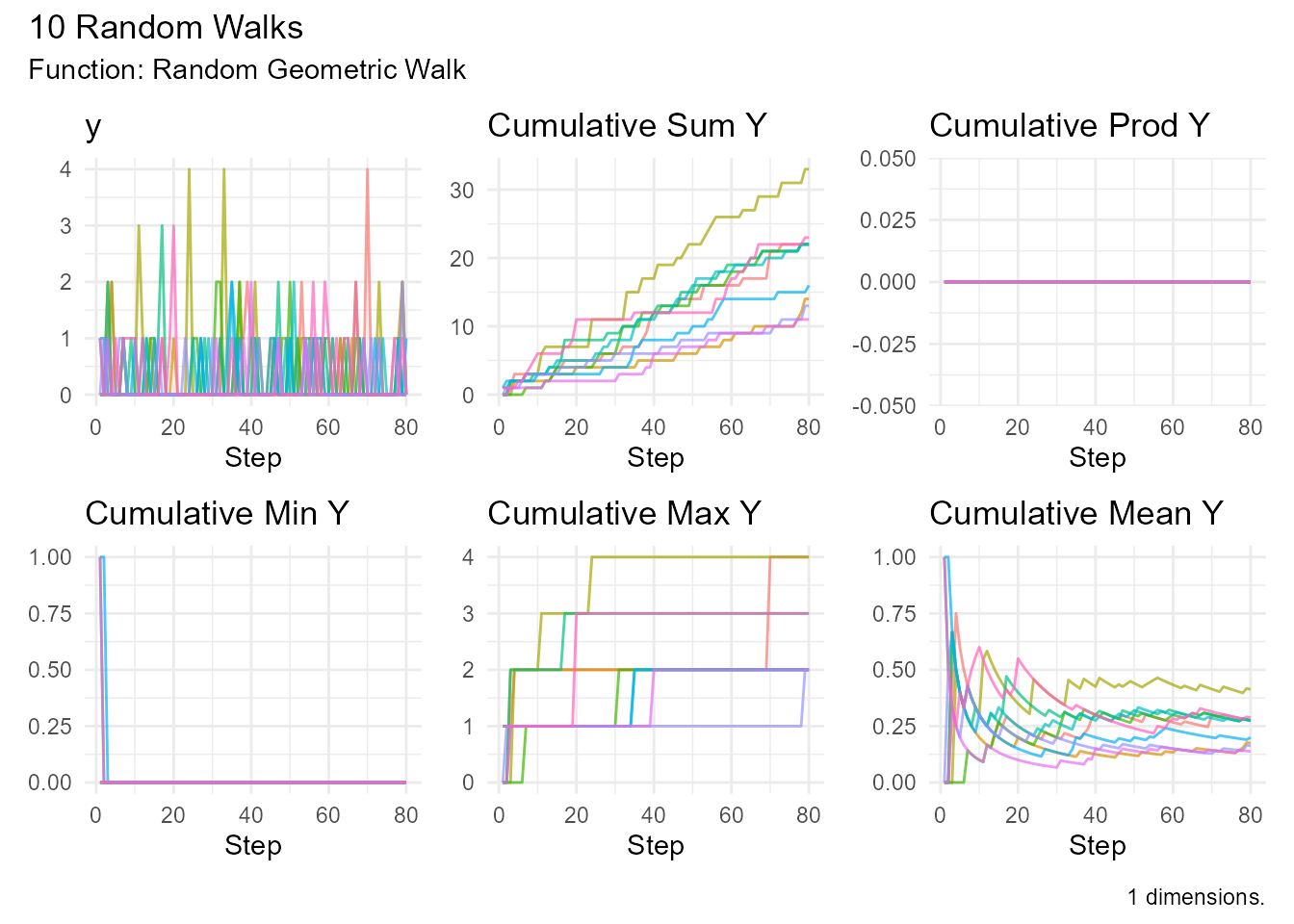

Geometric random walk with high probability showing short waiting times

# Customer conversion modeling
conversion <- random_geometric_walk(
  .num_walks = 100,
  .n = 50,
  .prob = 0.05  # 5% conversion rate
)

conversion |>
  summarize_walks(.value = y) |>
  pull(mean_val)  # Average trials until conversion
#> [1] 19.13025

Hypergeometric Distribution

`random_hypergeometric_walk()`

Random walk for sampling without replacement.

Function Signature:

random_hypergeometric_walk(
  .num_walks = 25,
  .nn = 100,
  .m = 50,
  .n = 50,
  .k = 10,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .m - Number of white balls in urn - .n - Number of black balls in urn - .k - Number of balls drawn

Properties: - Sampling without replacement - Mean = k × m / (m + n) - Used for finite populations

Use Cases: - Quality control sampling - Lottery probabilities - Card games - Ecological sampling

Example:

# Drawing from an urn
random_hypergeometric_walk(
  .num_walks = 10,
  .m = 50,      # 50 white balls
  .n = 50,  # 50 black balls
  .k = 10       # Draw 10 balls
) |> visualize_walks()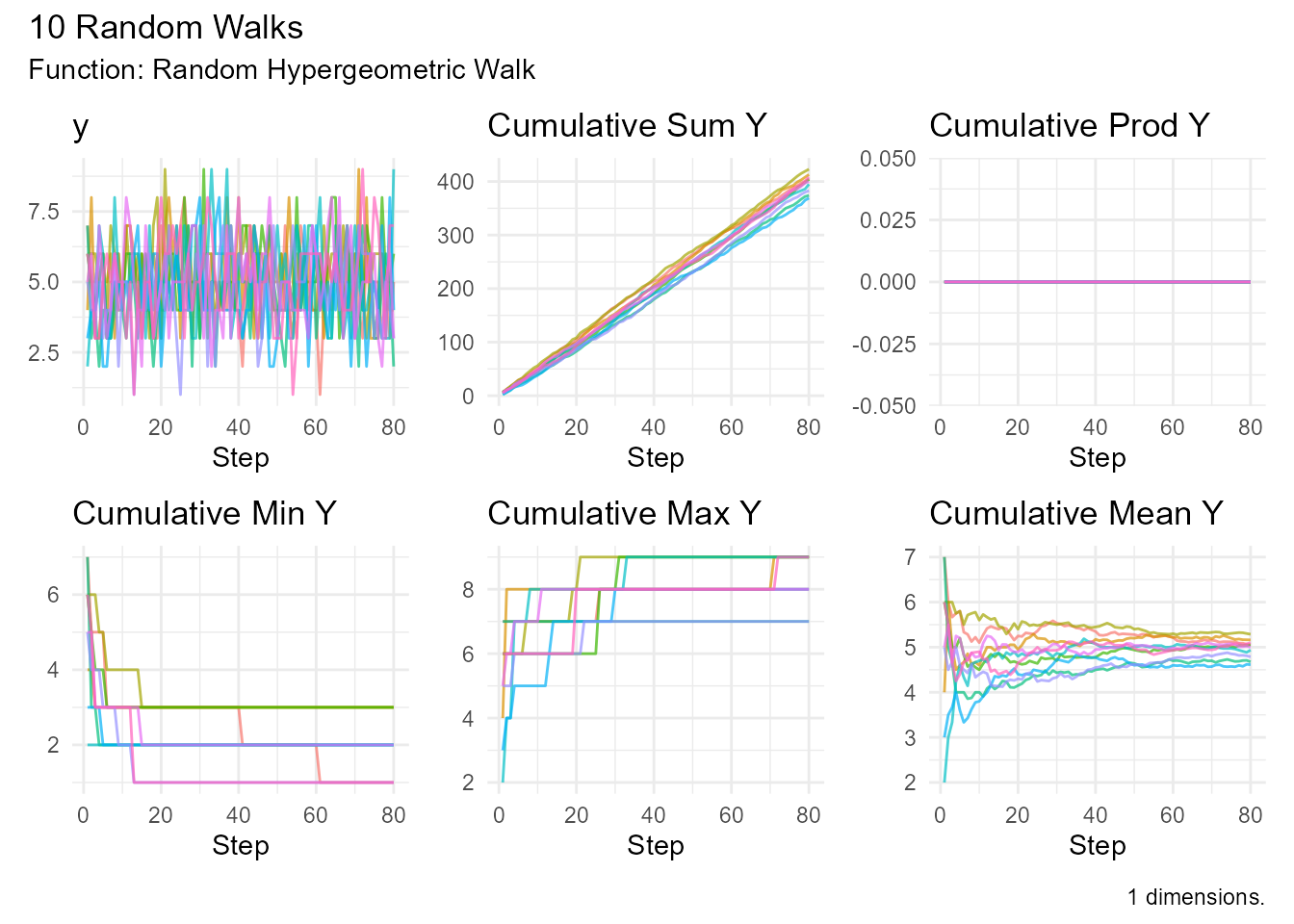

Hypergeometric random walk simulating drawing from an urn

# Quality inspection
inspection <- random_hypergeometric_walk(
  .num_walks = 100,
  .nn = 50,
  .m = 5,        # 5 defective items
  .n = 95,       # 95 good items
  .k = 10        # Sample 10 items
)

inspection |>
  summarize_walks(.value = y) |>
  pull(mean_val)  # Average defects found per sample
#> [1] 0.505

Multinomial Distribution

`random_multinomial_walk()`

Random walk with multiple outcome categories.

Function Signature:

random_multinomial_walk(
  .num_walks = 25,
  .n = 100,
  .size = 3,
  .prob = rep(1/3, .n),
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .size - Number of trials - .prob - Vector of probabilities (must sum to 1)

Properties: - Extension of binomial to multiple categories - Returns counts for each category - Probabilities must sum to 1

Use Cases: - Survey responses with multiple choices - Dice rolling - Market share analysis - Classification results

Example:

# Dice rolling (6 outcomes)
random_multinomial_walk(
  .num_walks = 10,
  .n = 100,  # Roll 100 times
  .size = 1,  # One die per roll
  .prob = rep(1/6, 100)  # Fair die: 6 categories
) |> visualize_walks()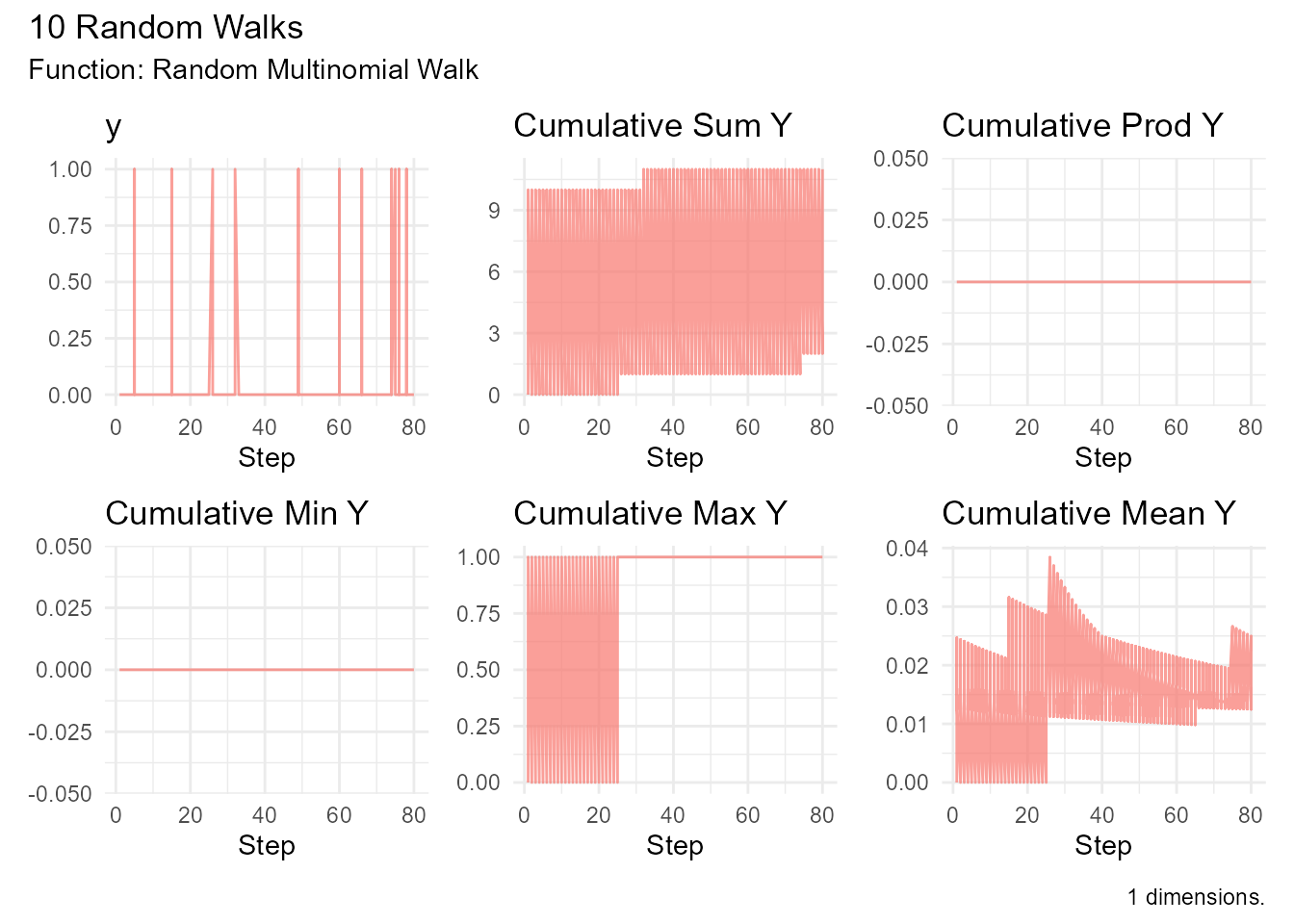

Multinomial random walk simulating dice rolling outcomes

# Market share simulation
market_share <- random_multinomial_walk(
  .num_walks = 50,
  .n = 52,  # Weekly for a year
  .size = 1000,  # Total customers
  .prob = rep(c(0.2, 0.2, 0.35, 0.25), 13)  # Four competitors
)

market_share |> visualize_walks()
#> Warning: Removed 45 rows containing missing values or values outside the scale range
#> (`geom_line()`).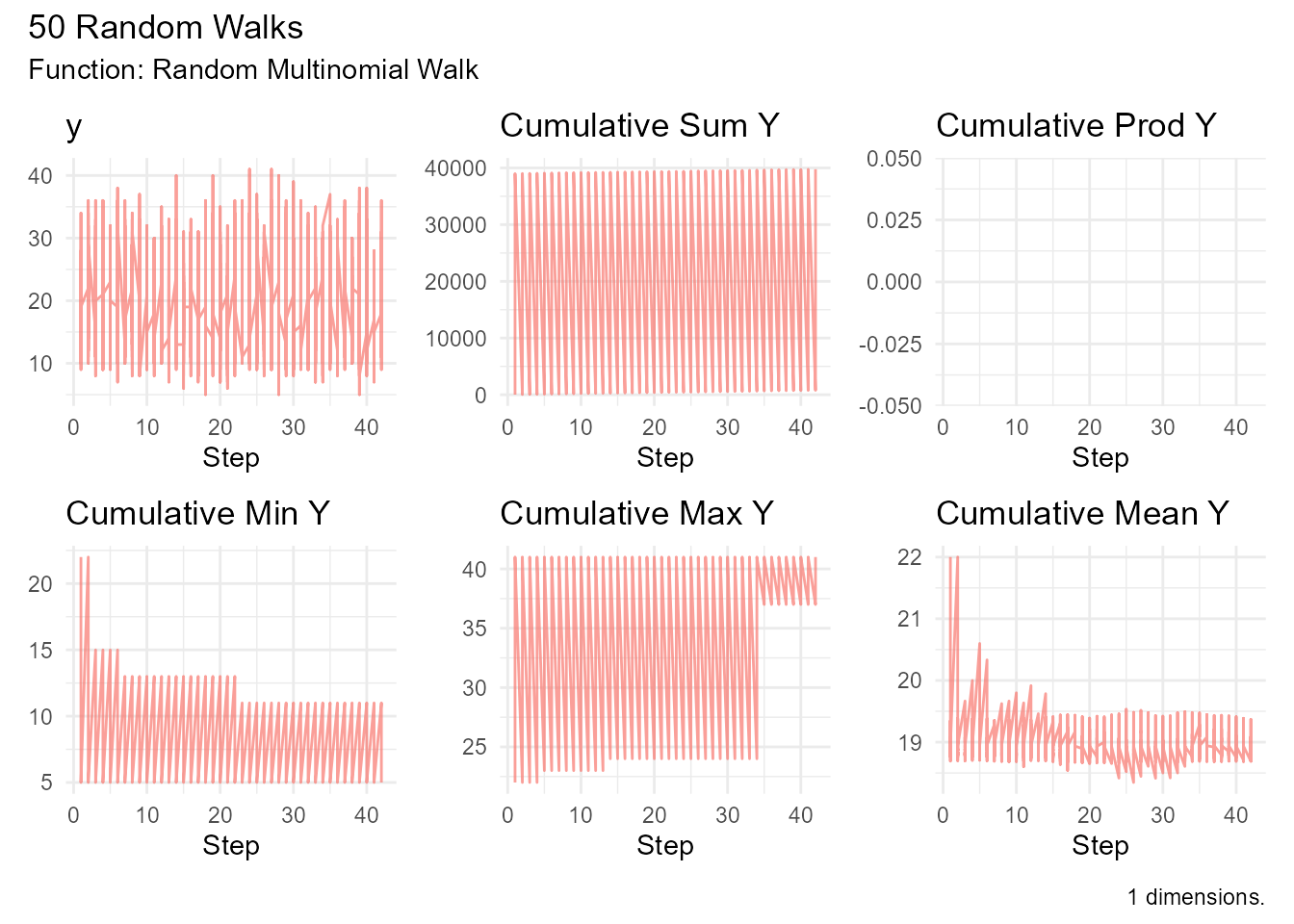

Market share simulation using multinomial distribution

Negative Binomial Distribution

`random_negbinomial_walk()`

Random walk based on negative binomial (number of failures before r successes).

Function Signature:

random_negbinomial_walk(
  .num_walks = 25,
  .n = 100,
  .size = 1,
  .prob = 0.5,
  .mu = NULL,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .size - Target number of successes - .prob - Probability of success - .mu - Alternative parameterization (mean)

Properties: - Overdispersed relative to Poisson - Mean = size × (1 - prob) / prob - Variance = size × (1 - prob) / prob²

Use Cases: - Overdispersed count data - Insurance claims - Accident modeling - Count data with extra variability

Example:

# Standard negative binomial
random_negbinomial_walk(
  .num_walks = 10,
  .size = 10,
  .prob = 0.5
) |> visualize_walks()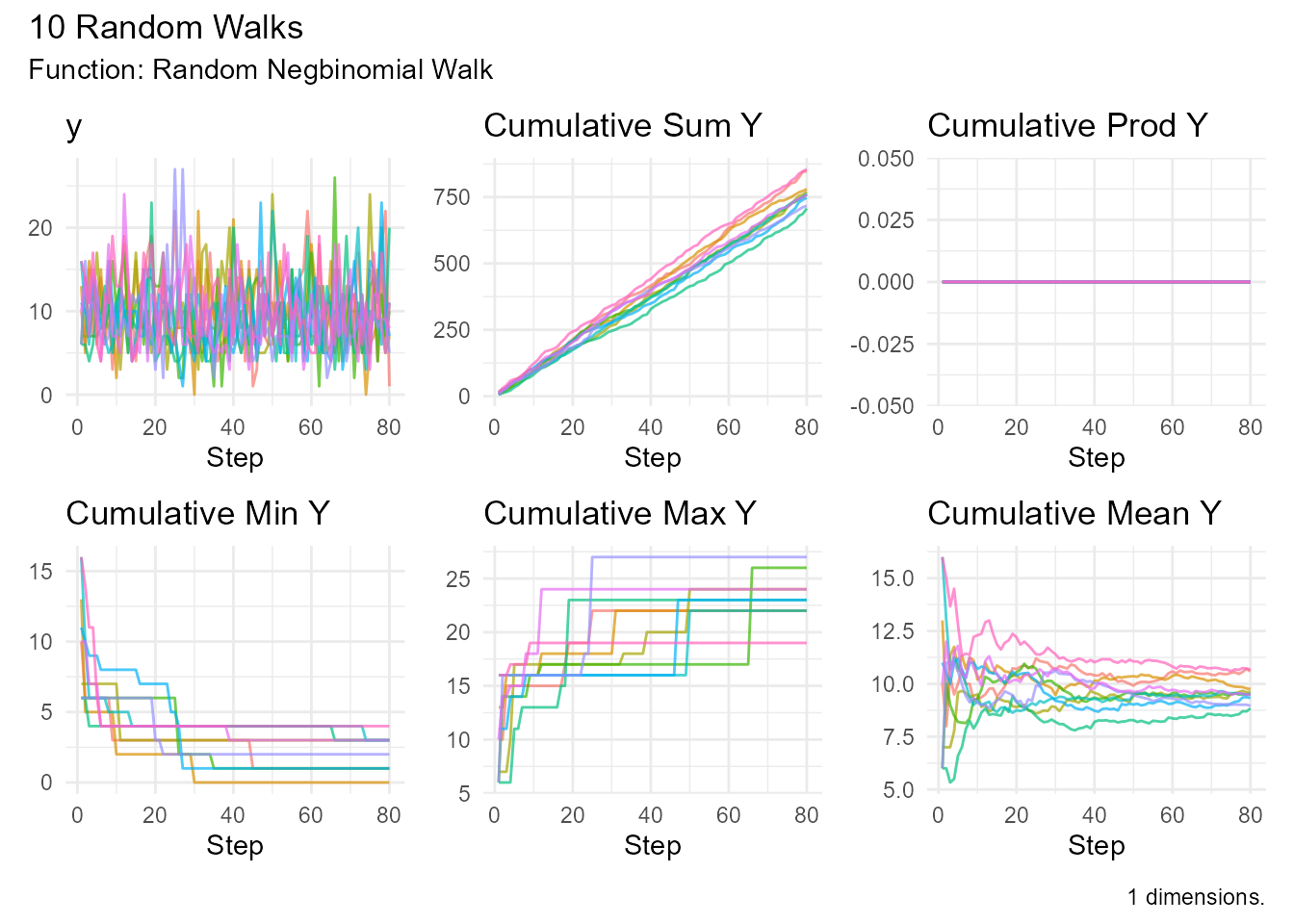

Negative binomial random walk showing overdispersed count data

# Overdispersed count data
claims <- random_negbinomial_walk(
  .num_walks = 100,
  .n = 12,  # Monthly
  .size = 5,
  .prob = 0.3
)

claims |>
  summarize_walks(.value = y, .group_var = walk_number) |>
  summarize(
    avg_monthly_claims = mean(mean_val),
    sd_monthly_claims = mean(sd)
  )
#> # A tibble: 1 × 2
#>   avg_monthly_claims sd_monthly_claims
#>                <dbl>             <dbl>
#> 1               11.9              6.04

Poisson Distribution

`random_poisson_walk()`

Random walk based on Poisson distribution (count of events in fixed interval).

Function Signature:

random_poisson_walk(
  .num_walks = 25,
  .n = 100,
  .lambda = 1,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .lambda - Rate parameter (mean and variance)

Properties: - Non-negative integer steps - Mean = Variance = λ - Approximates binomial for large n, small p

Use Cases: - Event counts (arrivals, calls, accidents) - Rare events - Queuing theory - Web traffic - Radioactive decay

Example:

# Low rate (rare events)
random_poisson_walk(
  .num_walks = 10,
  .lambda = 0.5
) |> visualize_walks()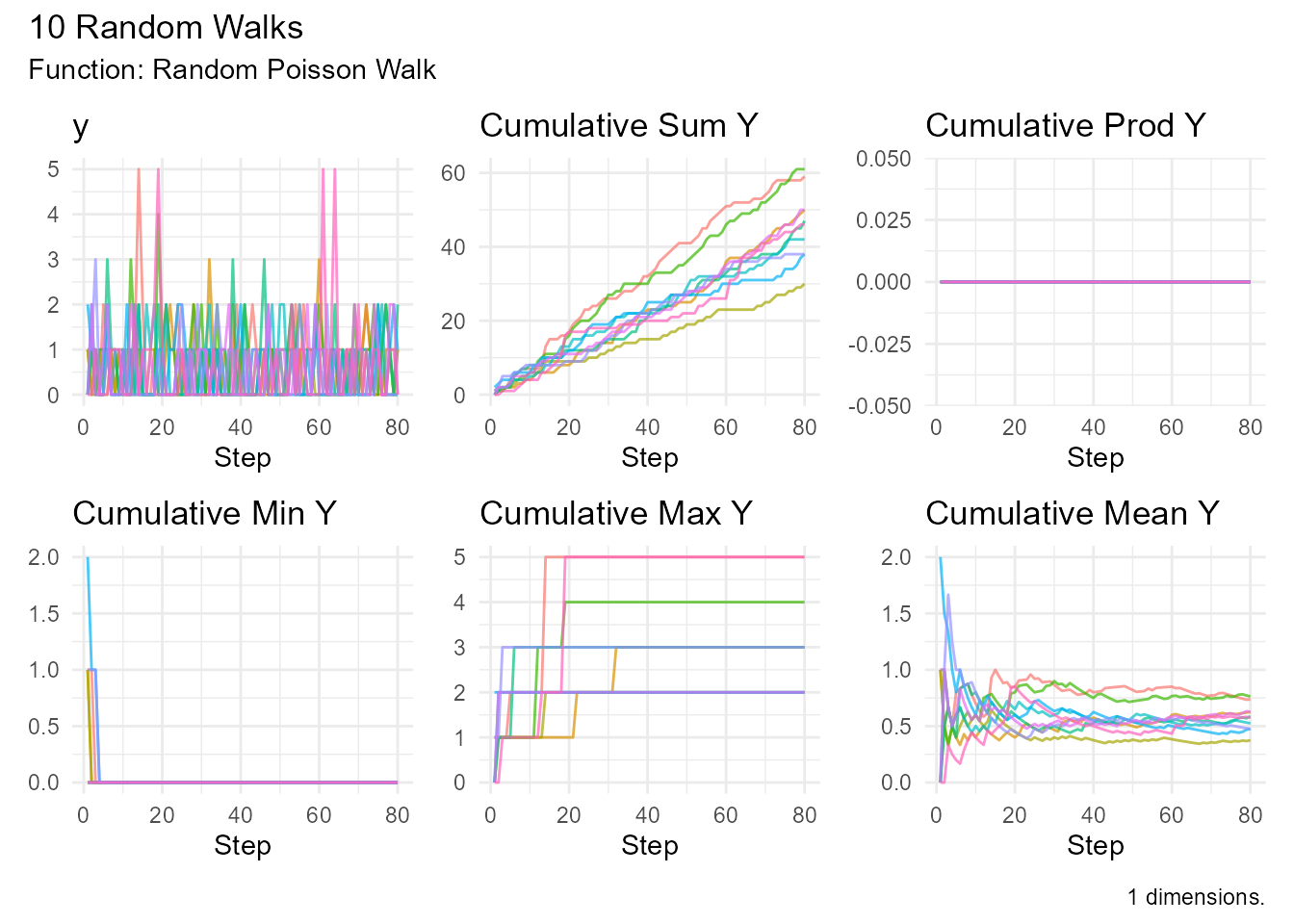

Poisson random walk with low rate showing rare events

# Call center arrivals
arrivals <- random_poisson_walk(
  .num_walks = 100,
  .n = 24,  # Hourly for a day
  .lambda = 15  # 15 calls per hour average
)

arrivals |>
  summarize_walks(.value = cum_sum_y, .group_var = walk_number) |>
  summarize(
    avg_daily_calls = mean(max_val),
    max_daily_calls = max(max_val),
    min_daily_calls = min(max_val)
  )
#> # A tibble: 1 × 3
#>   avg_daily_calls max_daily_calls min_daily_calls
#>             <dbl>           <dbl>           <dbl>
#> 1            283.             327             235

Wilcoxon Tests

`random_wilcox_walk()`

Random walk based on Wilcoxon rank sum statistic.

Function Signature:

random_wilcox_walk(
  .num_walks = 25,
  .n = 100,
  .m = 10,
  .k = 10,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .m - Number of observations in first group - .k - Number of observations in second group

Use Cases: - Nonparametric hypothesis testing - Rank-based statistics - Distribution-free methods

Example:

random_wilcox_walk(
  .num_walks = 10,
  .m = 20,
  .k = 10
) |> visualize_walks()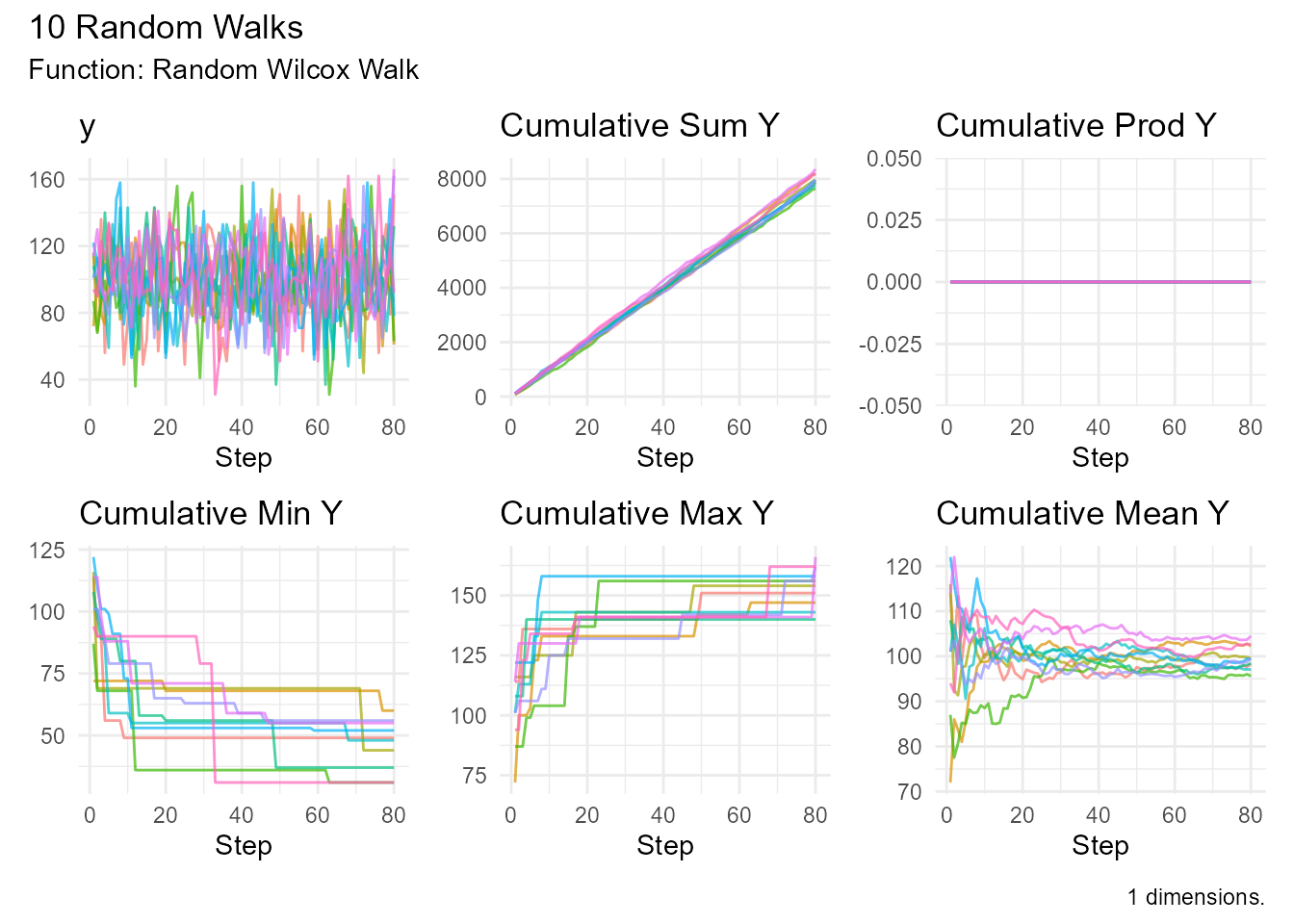

Wilcoxon rank sum random walk for nonparametric testing

`random_wilcoxon_sr_walk()`

Random walk based on Wilcoxon signed rank statistic.

Function Signature:

random_wilcoxon_sr_walk(
  .num_walks = 25,
  .nn = 100,
  .n = 1,
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .nn - Number of observations - .n - Integer or vector. Number(s) of observations in the sample(s) for rsignrank. Default is 1.

Use Cases: - Paired samples testing - Before/after comparisons - Matched pairs analysis

Example:

random_wilcoxon_sr_walk(
  .num_walks = 10,
  .n = 20
) |> visualize_walks()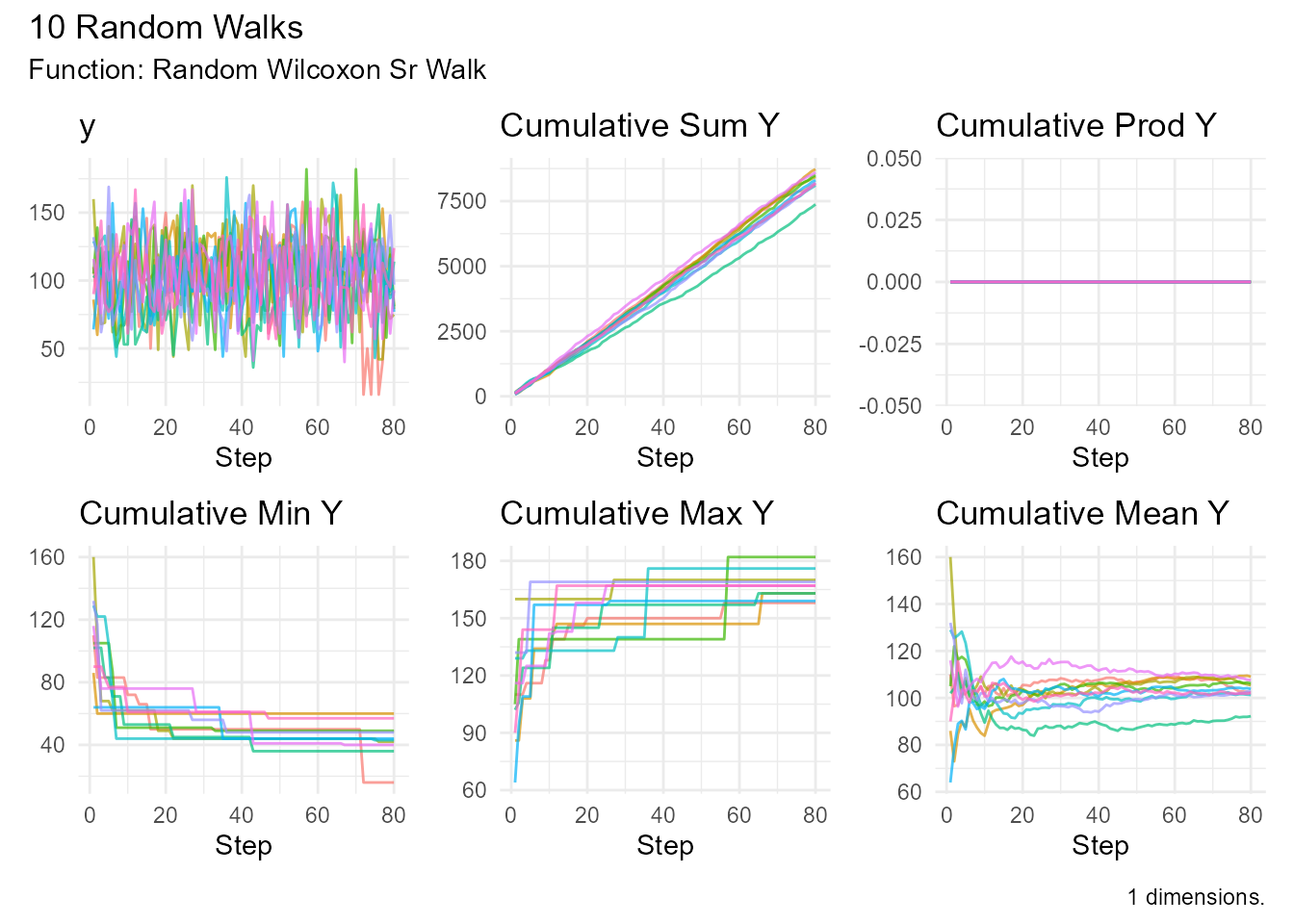

Wilcoxon signed rank random walk for paired samples testing

Smirnov Distribution

`random_smirnov_walk()`

Random walk based on Kolmogorov-Smirnov statistic distribution.

Function Signature:

random_smirnov_walk(
  .num_walks = 25,
  .n = 100,
  .sizes = c(1, 1),
  .z = NULL,
  .alternative = "two.sided",
  .initial_value = 0,
  .samp = TRUE,
  .replace = TRUE,
  .sample_size = 0.8,
  .dimensions = 1
)

Parameters: - .sizes - A numeric vector of length 2 specifying the sizes parameter for rsmirnov. Default is c(1, 1). - .z - Optional numeric vector for the z parameter in rsmirnov. Default is NULL. - .alternative - One of “two.sided” (default), “less”, or “greater”. Indicates the type of test statistic.

Use Cases: - Goodness-of-fit testing - Distribution comparison - Nonparametric statistics

Example:

random_smirnov_walk(
  .num_walks = 10,
  .sizes = c(5,10)
) |> visualize_walks()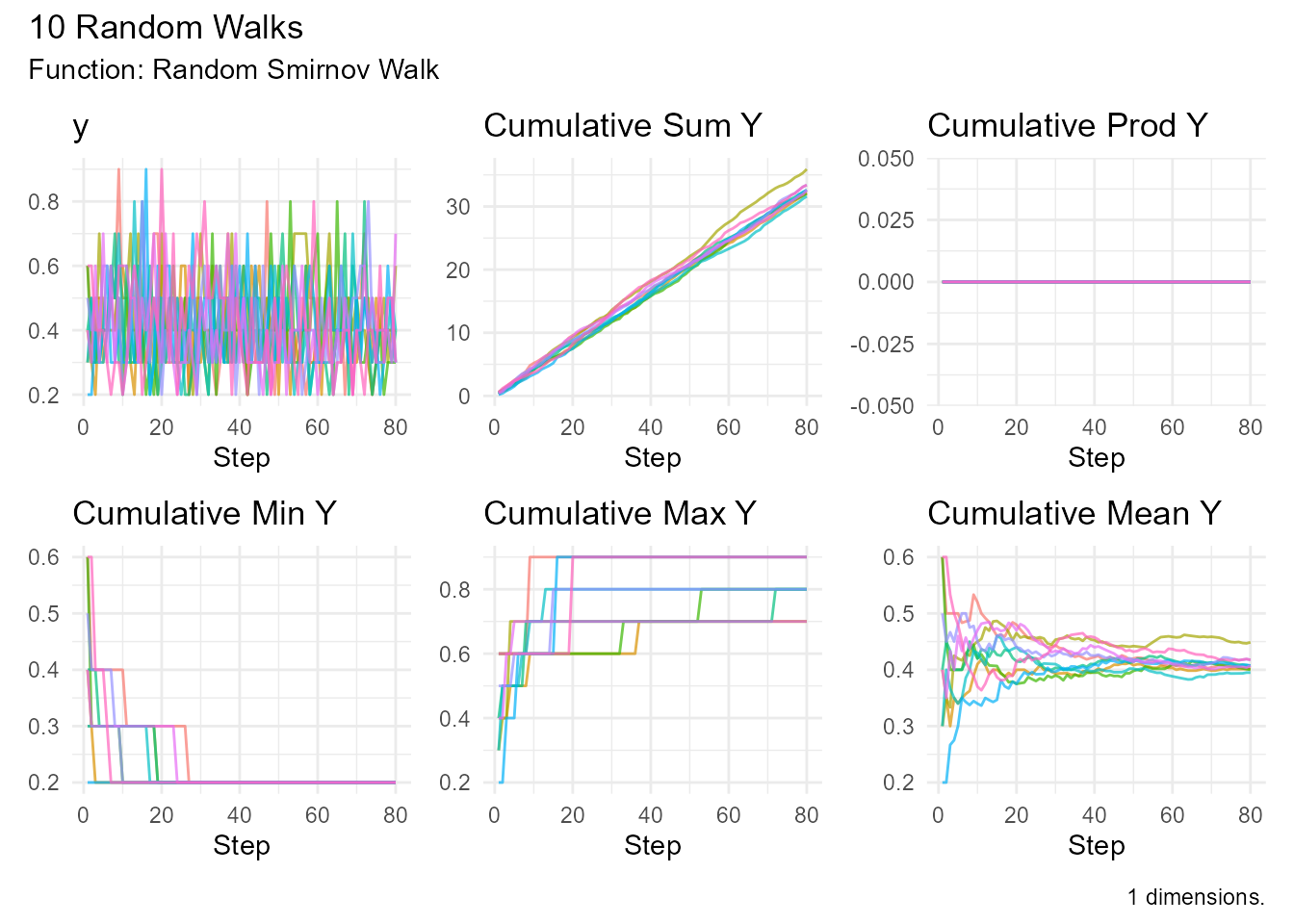

Smirnov distribution random walk for goodness-of-fit testing

Comparison Guide

When to Use Each Distribution

Distribution	Use When…	Key Property
Discrete Walk	Simple binary outcomes	Up or down with probability
Binomial	Counting successes in n trials	Fixed number of trials
Geometric	Time until first success	Memoryless property
Hypergeometric	Sampling without replacement	Finite population
Multinomial	Multiple outcome categories	Extension of binomial
Negative Binomial	Overdispersed count data	More variable than Poisson
Poisson	Event counts in interval	Mean = Variance
Wilcoxon	Nonparametric testing	Rank-based
Smirnov	Distribution comparison	Goodness-of-fit

Count Data Selection

Use Poisson when: - Mean ≈ Variance - Events are independent - Rate is constant

Use Negative Binomial when: - Variance > Mean (overdispersion) - Extra variability present - Poisson model doesn’t fit

Use Binomial when: - Fixed number of trials - Binary outcomes - Independent trials

Practical Examples

Example 1: Website Traffic

# Daily page views (Poisson)
traffic <- random_poisson_walk(
  .num_walks = 100,
  .n = 365,  # Days in year
  .lambda = 1000  # Average daily views
)

# Visualize cumulative page views for a sample of walks
traffic |>
  dplyr::filter(walk_number %in% levels(traffic$walk_number)[1:10]) |>
  visualize_walks(.pluck = "cum_sum") +
  ggplot2::labs(
    title = "Cumulative Website Page Views (Poisson Random Walk)",
    x = "Day",
    y = "Cumulative Page Views"
  )

Website traffic modeling using Poisson distribution


# Compute total annual views (summary statistic)
traffic |>
  summarize_walks(.value = cum_sum_y) |>
  dplyr::pull(max_val) |>
  mean()  # Total annual views
#> [1] 294053

Example 2: Quality Control

# Defect sampling (Hypergeometric)
quality <- random_hypergeometric_walk(
  .num_walks = 1000,
  .nn = 50,  # 50 inspections
  .m = 10,   # 10 defective in lot
  .n = 90,  # 90 good in lot
  .k = 5     # Sample 5 items
)

quality |>
  summarize_walks(.value = y, .group_var = walk_number) |>
  dplyr::summarize(
    prob_find_defect = mean(max_val > 0)
  )
#> # A tibble: 1 × 1
#>   prob_find_defect
#>              <dbl>
#> 1                1

Example 3: Customer Service

# Calls until resolution (Geometric)
resolution <- random_geometric_walk(
  .num_walks = 500,
  .n = 100,
  .prob = 0.15  # 15% resolution rate per call
)

resolution |>
  summarize_walks(.value = y) |>
  pull(mean_val)  # Average calls until resolution
#> [1] 5.67865

Best Practices

Choosing Parameters

Understand your data
- Is it count data or binary?
- Is there overdispersion?
- Is the population finite or infinite?
Match the distribution to the process
- Time between events → Geometric or Poisson
- Success counting → Binomial or Negative Binomial
- Sampling → Hypergeometric
Consider practical constraints
- Finite population → Hypergeometric
- Overdispersion → Negative Binomial
- Simple binary → Discrete Walk

Validation

# Check if distribution fits your expectations
walk <- random_poisson_walk(.num_walks = 1000, .n = 100, .lambda = 5)

walk |>
  summarize_walks(.value = y) |>
  summarize(
    empirical_mean = mean_val,
    empirical_var = variance,
    ratio = variance / mean_val  # Should be ≈ 1 for Poisson
  )
#> # A tibble: 1 × 3
#>   empirical_mean empirical_var ratio
#>            <dbl>         <dbl> <dbl>
#> 1           5.02          5.05  1.01

Next Steps

Continuous Distribution Generators - Explore continuous distributions
Visualization Guide - Create beautiful plots
Statistical Analysis Guide - Analyze your walks
Use Cases and Examples - Real-world applications

Need more examples? Check out the package documentation and vignettes!

Table of Contents

Common Parameters

Discrete Walk

discrete_walk()

Binomial Distribution

random_binomial_walk()

Geometric Distribution

random_geometric_walk()

Hypergeometric Distribution

random_hypergeometric_walk()

Multinomial Distribution

random_multinomial_walk()

Negative Binomial Distribution

random_negbinomial_walk()

Poisson Distribution

random_poisson_walk()

Wilcoxon Tests

random_wilcox_walk()

random_wilcoxon_sr_walk()

Smirnov Distribution

random_smirnov_walk()

Comparison Guide

When to Use Each Distribution

Count Data Selection

Practical Examples

Example 1: Website Traffic

Example 2: Quality Control

Example 3: Customer Service

Best Practices

Choosing Parameters

Validation

Next Steps

`discrete_walk()`

`random_binomial_walk()`

`random_geometric_walk()`

`random_hypergeometric_walk()`

`random_multinomial_walk()`

`random_negbinomial_walk()`

`random_poisson_walk()`

`random_wilcox_walk()`

`random_wilcoxon_sr_walk()`

`random_smirnov_walk()`