Core Concepts

library(TidyDensity)
library(dplyr)
library(ggplot2)
library(patchwork)
library(withr)

Understanding the fundamental concepts behind TidyDensity will help you use the package effectively.

Tidy Data Philosophy

What is Tidy Data?

Tidy data follows three principles:

1. Each variable is a column
2. Each observation is a row
3. Each type of observational unit is a table

Why Tidy Data Matters

# Traditional approach (base R)
x <- rnorm(100)
# Just a vector - limited functionality

# TidyDensity approach
data <- tidy_normal(.n = 100)
# A tibble with structure:
# - sim_number: simulation ID
# - x: observation number
# - y: random value
# - dx, dy: density values
# - p: cumulative probability
# - q: quantile

head(data)
#> # A tibble: 6 × 7
#>   sim_number     x      y    dx       dy      p      q
#>   <fct>      <int>  <dbl> <dbl>    <dbl>  <dbl>  <dbl>
#> 1 1              1 -0.387 -2.99 0.000241 0.349  -0.387
#> 2 1              2 -0.785 -2.92 0.000431 0.216  -0.785
#> 3 1              3 -1.06  -2.86 0.000743 0.145  -1.06 
#> 4 1              4 -0.796 -2.79 0.00125  0.213  -0.796
#> 5 1              5 -1.76  -2.72 0.00202  0.0395 -1.76 
#> 6 1              6 -0.691 -2.65 0.00318  0.245  -0.691

Benefits of Tidy Format

1. Pipeable:

tidy_normal(.n = 100) |>
  filter(y > 0) |>
  summarise(mean = mean(y), sd = sd(y))
#> # A tibble: 1 × 2
#>    mean    sd
#>   <dbl> <dbl>
#> 1 0.788 0.651

2. Visualization-ready:

tidy_normal(.n = 100) |>
  tidy_autoplot(.plot_type = "density")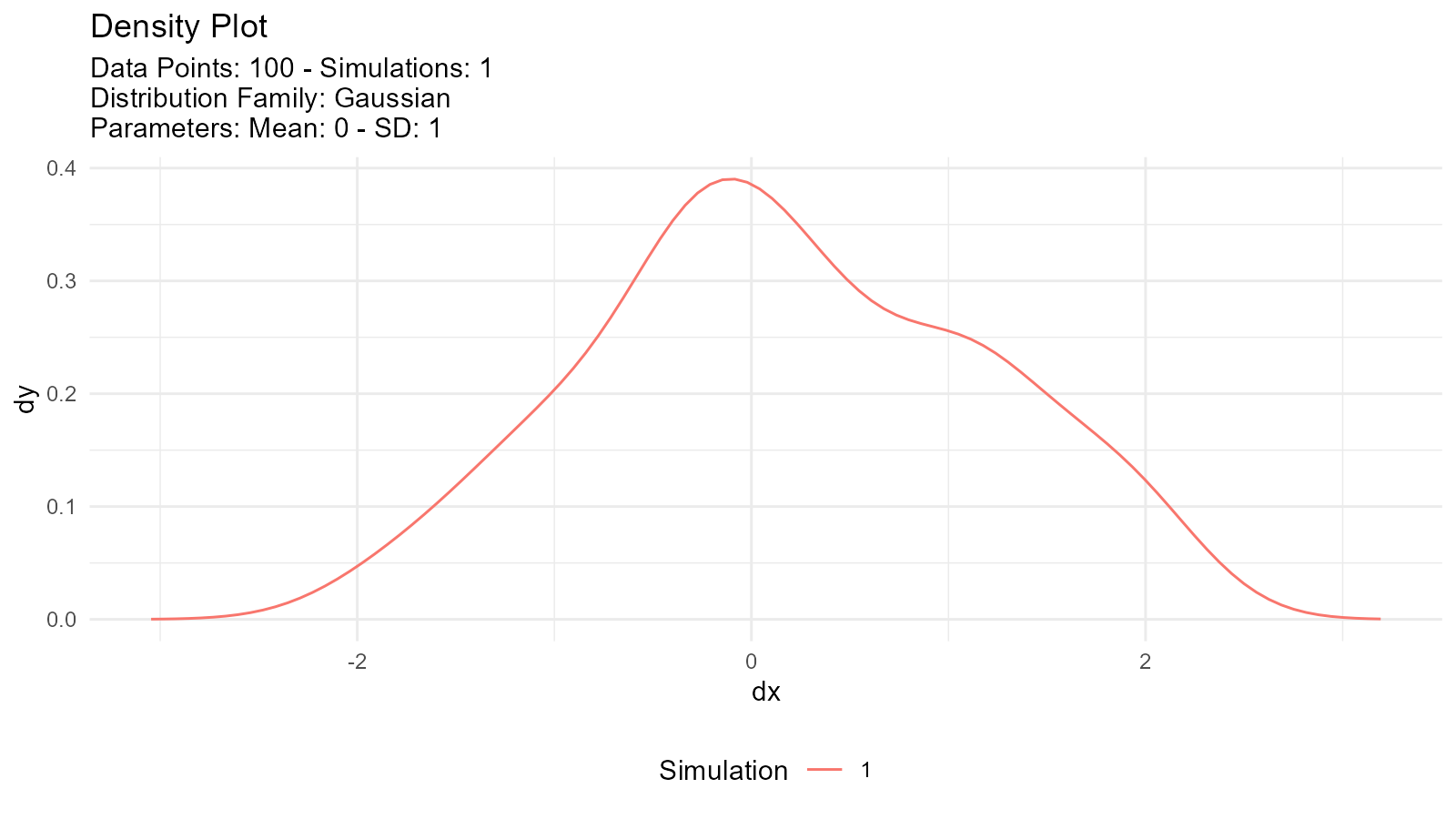

3. Analysis-friendly:

tidy_normal(.n = 100, .num_sims = 10) |>
  group_by(sim_number) |>
  summarise(mean = mean(y))
#> # A tibble: 10 × 2
#>    sim_number    mean
#>    <fct>        <dbl>
#>  1 1          -0.177 
#>  2 2          -0.0517
#>  3 3          -0.163 
#>  4 4           0.0554
#>  5 5          -0.102 
#>  6 6           0.138 
#>  7 7          -0.147 
#>  8 8          -0.207 
#>  9 9          -0.0922
#> 10 10          0.0844

Probability Distributions

What is a Probability Distribution?

A probability distribution describes how values of a random variable are distributed.

Types of Distributions

Continuous Distributions

Values can take any real number within a range:

# Normal distribution
normal_data <- tidy_normal(.n = 100, .mean = 0, .sd = 1)

# Uniform distribution
uniform_data <- tidy_uniform(.n = 100, .min = 0, .max = 1)

# Visualize both
p1 <- tidy_autoplot(normal_data, .plot_type = "density") +
  ggtitle("Normal Distribution")
p2 <- tidy_autoplot(uniform_data, .plot_type = "density") +
  ggtitle("Uniform Distribution")

p1 | p2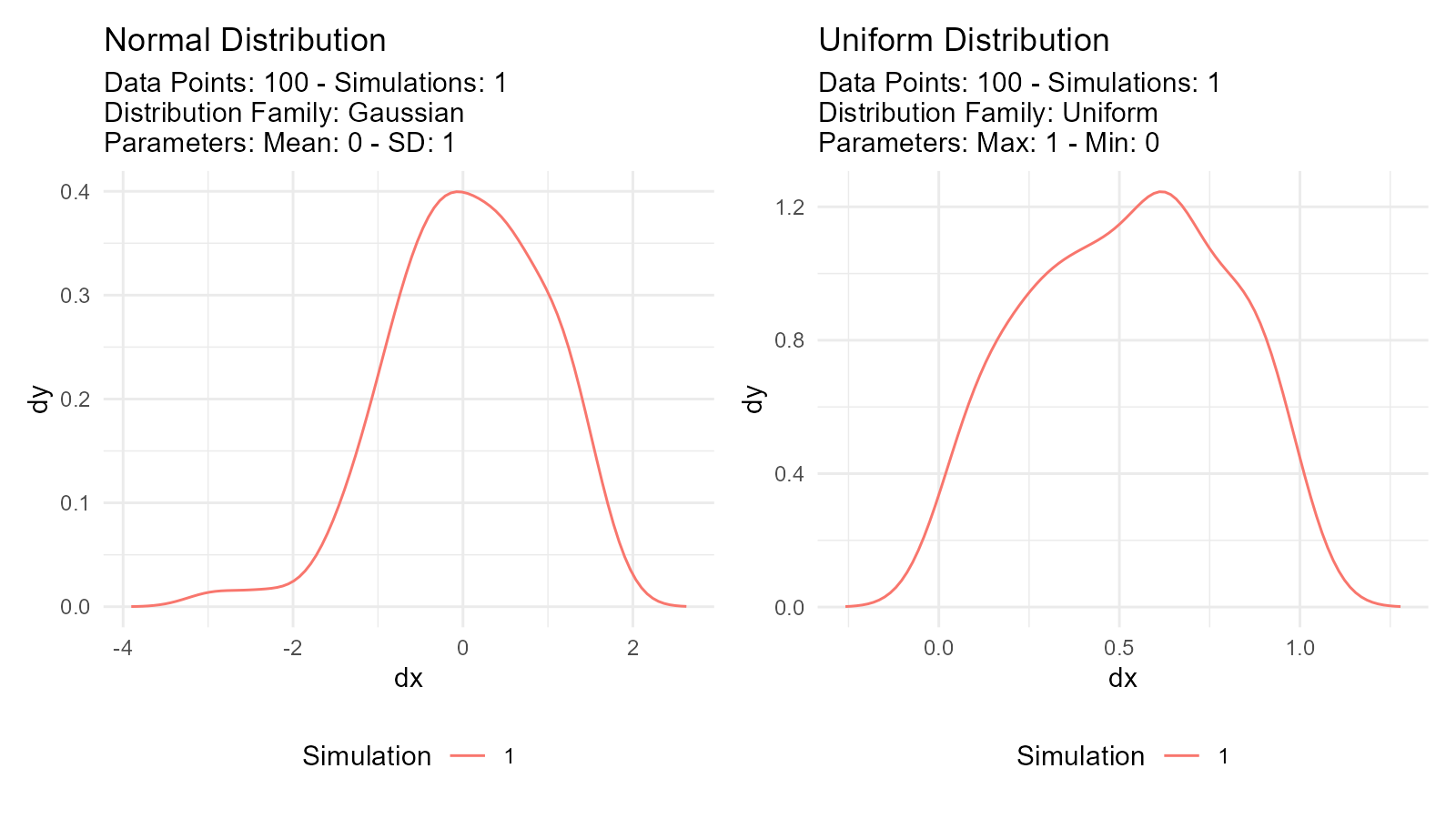

Discrete Distributions

Values can only take specific integers:

# Poisson distribution
poisson_data <- tidy_poisson(.n = 100, .lambda = 5)

# Binomial distribution
binomial_data <- tidy_binomial(.n = 100, .size = 10, .prob = 0.5)

# Visualize both
p1 <- tidy_autoplot(poisson_data, .plot_type = "density") +
  ggtitle("Poisson Distribution")
p2 <- tidy_autoplot(binomial_data, .plot_type = "density") +
  ggtitle("Binomial Distribution")

p1 | p2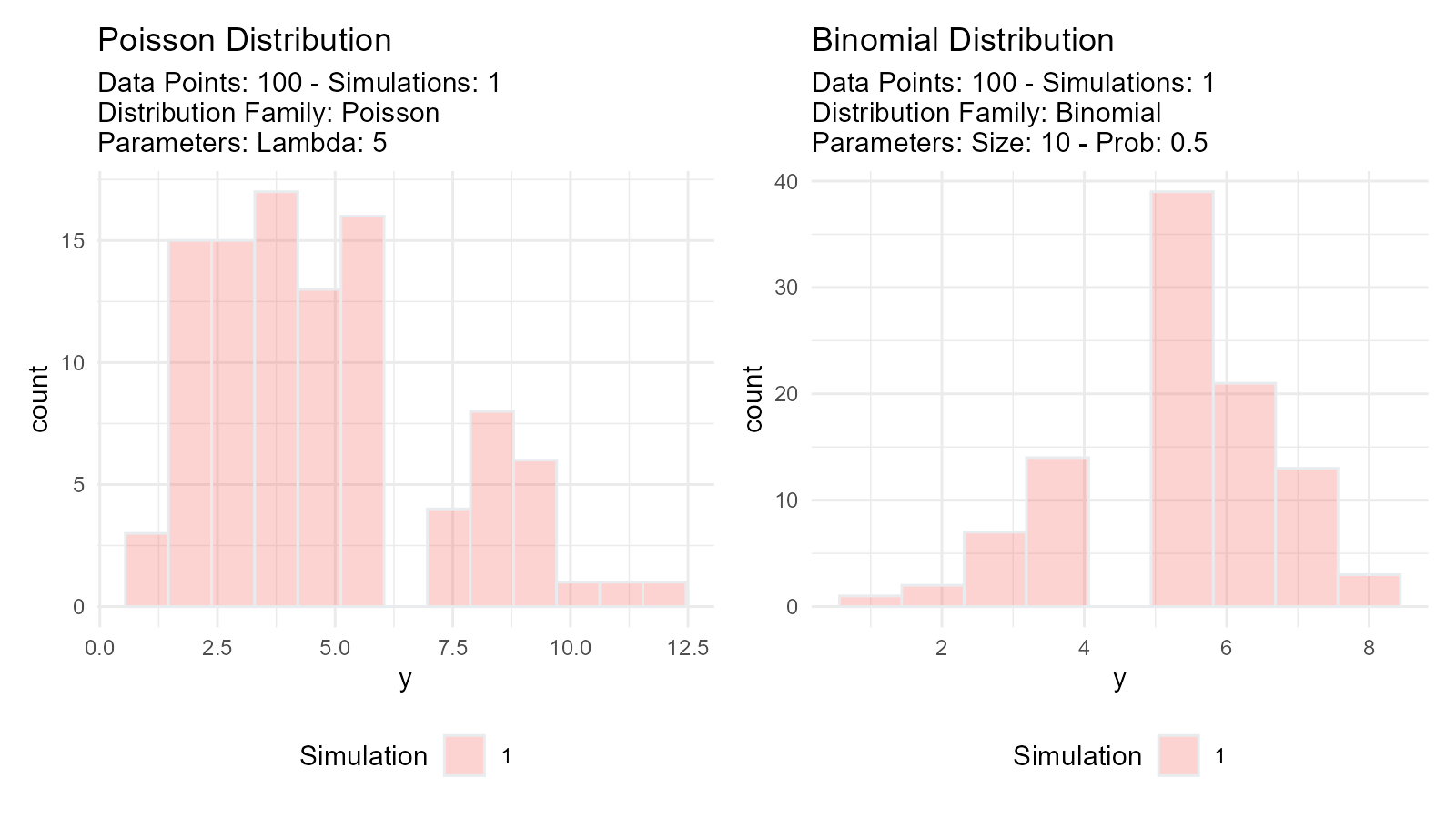

Distribution Characteristics

Location (Center): - Where the distribution is centered - Examples: mean, median, mode

Scale (Spread): - How spread out the values are - Examples: standard deviation, variance, IQR

Shape: - Form of the distribution - Examples: skewness, kurtosis, modality

# Normal: Symmetric, bell-shaped
normal <- tidy_normal(.n = 100, .mean = 0, .sd = 1)

# Gamma: Right-skewed
gamma <- tidy_gamma(.n = 100, .shape = 2, .scale = 1)

# Uniform: Flat, all values equally likely
uniform <- tidy_uniform(.n = 100, .min = 0, .max = 1)

# Visualize characteristics
p1 <- tidy_autoplot(normal, .plot_type = "density") +
  ggtitle("Normal: Symmetric")
p2 <- tidy_autoplot(gamma, .plot_type = "density") +
  ggtitle("Gamma: Right-skewed")
p3 <- tidy_autoplot(uniform, .plot_type = "density") +
  ggtitle("Uniform: Flat")

p1 | p2 | p3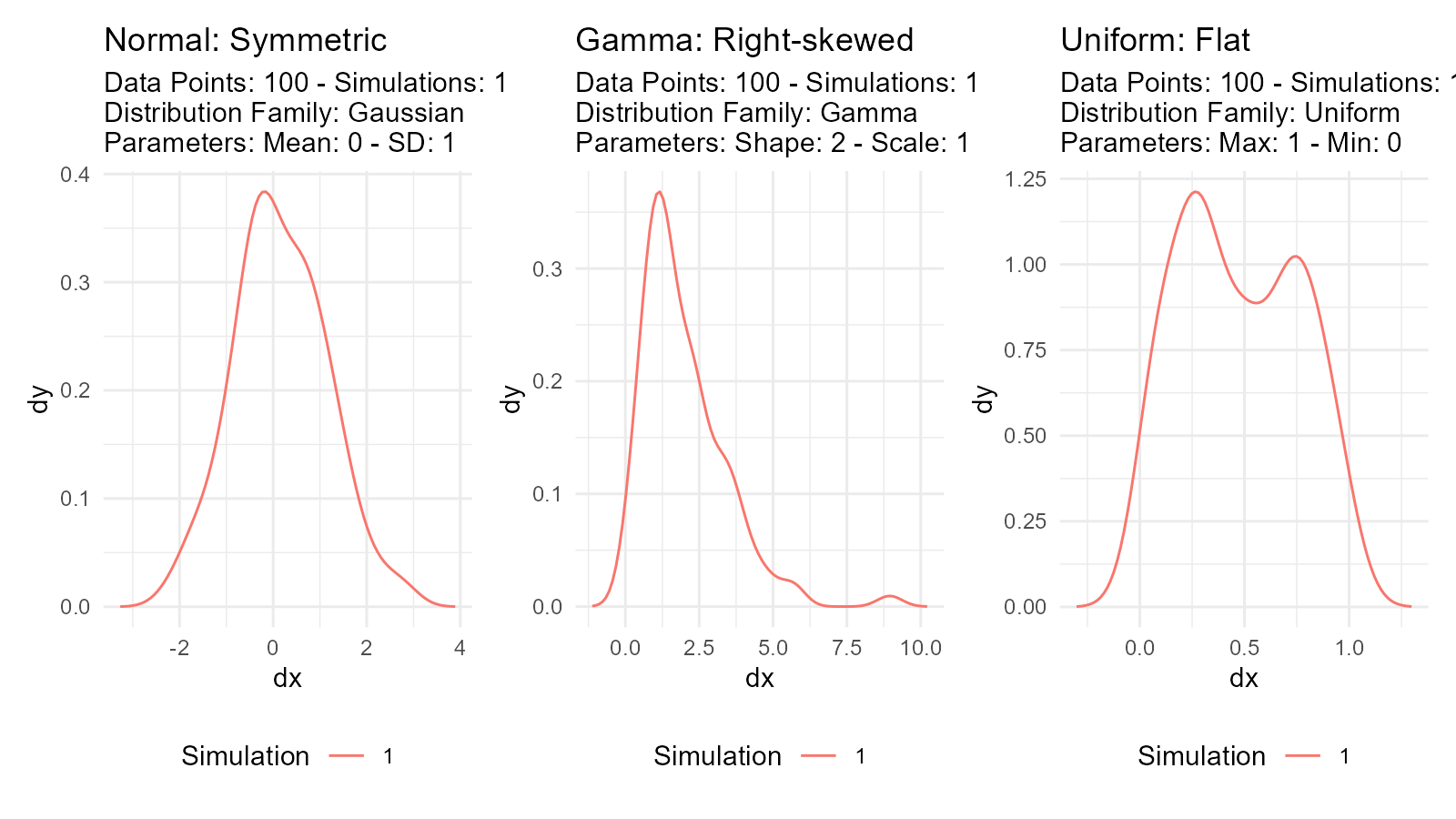

Distribution Functions (d, p, q, r)

Every probability distribution has four related functions:

1. Density Function (d)

Probability Density Function (PDF) for continuous distributions: - How likely is a specific value? - In TidyDensity: dy column

data <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
# dy column contains density values
head(data[, c("y", "dy")])
#> # A tibble: 6 × 2
#>        y       dy
#>    <dbl>    <dbl>
#> 1 -1.05  0.000147
#> 2 -1.38  0.000288
#> 3  0.479 0.000533
#> 4 -0.114 0.000941
#> 5 -0.603 0.00158 
#> 6 -0.630 0.00254

2. Probability Function (p)

Cumulative Distribution Function (CDF): - What’s the probability of getting a value ≤ x? - In TidyDensity: p column

data <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
# p column contains cumulative probabilities
# p = 0.5 means 50% of values are below this point
head(data[, c("y", "p")])
#> # A tibble: 6 × 2
#>         y     p
#>     <dbl> <dbl>
#> 1 -0.566  0.286
#> 2  1.67   0.952
#> 3 -0.126  0.450
#> 4  1.21   0.886
#> 5 -0.0960 0.462
#> 6 -1.03   0.150

3. Quantile Function (q)

Inverse of CDF (Quantile Function): - What value corresponds to a given probability? - In TidyDensity: q column

data <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
# q column contains quantile values
# q at p=0.5 gives the median
head(data[, c("p", "q")])
#> # A tibble: 6 × 2
#>       p      q
#>   <dbl>  <dbl>
#> 1 0.293 -0.545
#> 2 0.405 -0.239
#> 3 0.834  0.970
#> 4 0.702  0.531
#> 5 0.612  0.284
#> 6 0.294 -0.542

4. Random Generation Function (r)

Generate random values: - Simulate data from the distribution - In TidyDensity: y column

data <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
# y column contains randomly generated values
head(data[, c("x", "y")])
#> # A tibble: 6 × 2
#>       x      y
#>   <int>  <dbl>
#> 1     1 -1.17 
#> 2     2  1.01 
#> 3     3  0.594
#> 4     4 -1.00 
#> 5     5  1.25 
#> 6     6 -0.130

Visual Comparison

data <- tidy_normal(.n = 100, .num_sims = 1)

# Density plot (d function)
p1 <- tidy_autoplot(data, .plot_type = "density") +
  ggtitle("Density (d)")

# CDF plot (p function)
p2 <- tidy_autoplot(data, .plot_type = "probability") +
  ggtitle("Probability (p)")

# Quantile plot (q function)
p3 <- tidy_autoplot(data, .plot_type = "quantile") +
  ggtitle("Quantile (q)")

# Combined view
(p1 | p2) / p3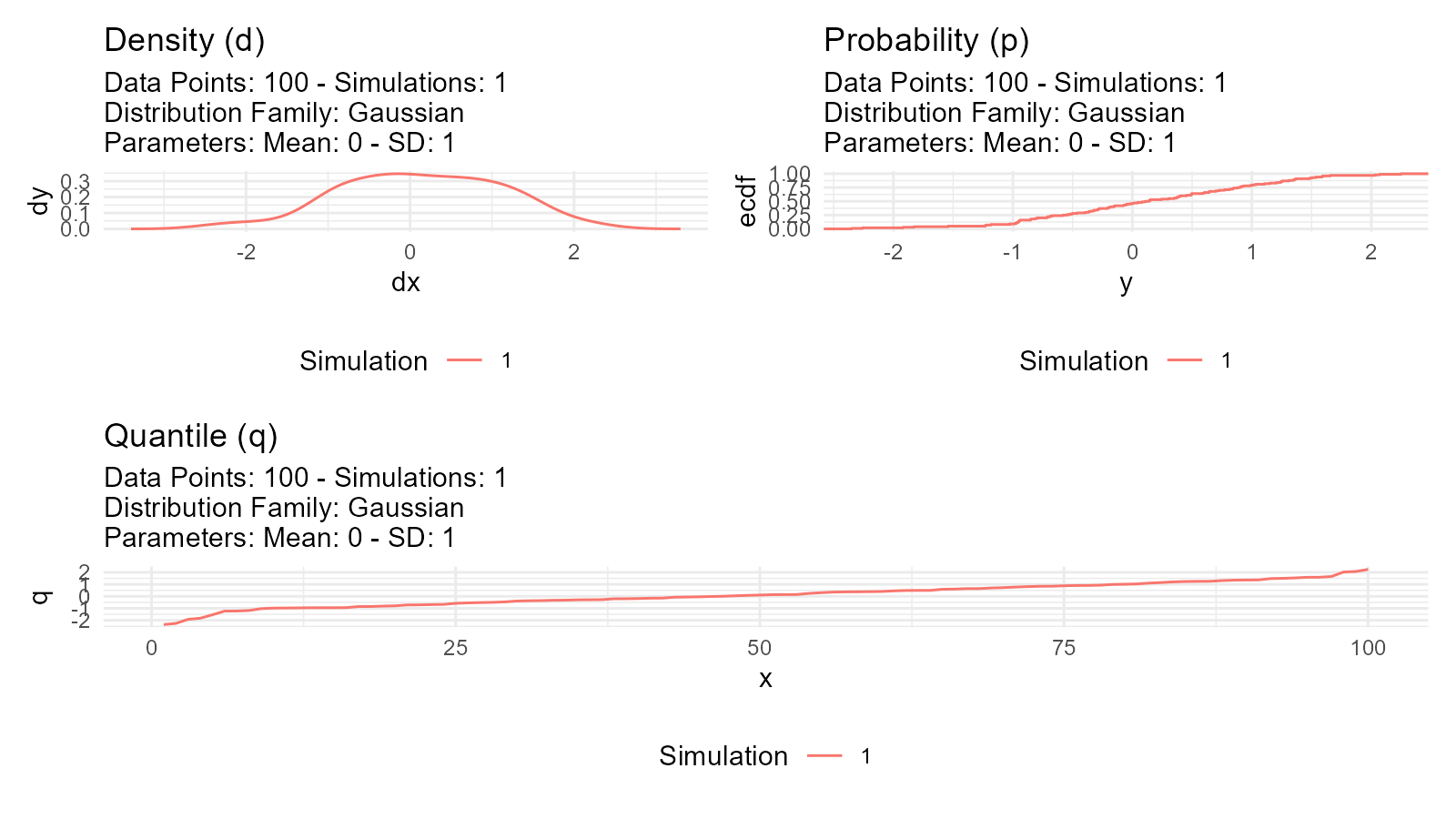

Random Number Generation

Pseudorandom Numbers

Computer-generated “random” numbers are actually pseudorandom: - Deterministic algorithm - Appears random but reproducible with same seed - Good enough for most applications

Setting Seeds for Reproducibility

# Use withr::with_seed() for reproducible results
data1 <- withr::with_seed(123, tidy_normal(.n = 10))

data2 <- withr::with_seed(123, tidy_normal(.n = 10))

# data1 and data2 are identical
all.equal(data1$y, data2$y)
#> [1] TRUE

Multiple Simulations

Why use multiple simulations?

# Single simulation - might not represent true distribution
single <- tidy_normal(.n = 100, .num_sims = 1)

# Multiple simulations - better understanding of variability
multiple <- tidy_normal(.n = 100, .num_sims = 20)

p1 <- tidy_autoplot(single, .plot_type = "density") +
  ggtitle("Single Simulation")
p2 <- tidy_autoplot(multiple, .plot_type = "density") +
  ggtitle("20 Simulations")

p1 | p2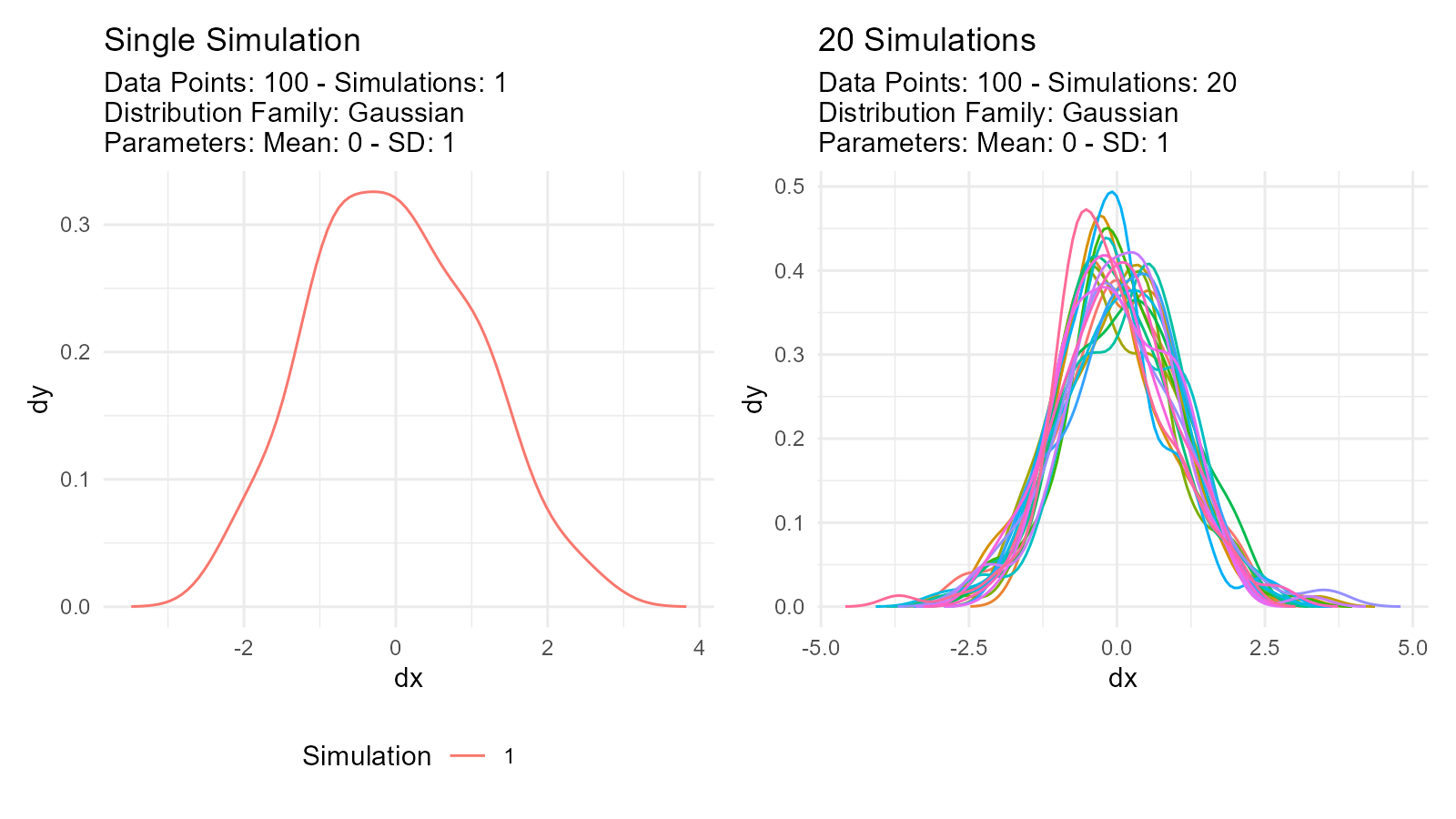

Use cases: - Assess sampling variability - Monte Carlo simulation - Sensitivity analysis - Uncertainty quantification

Parameter Estimation

What is Parameter Estimation?

Goal: Estimate distribution parameters from observed data

# Observed data
observed <- c(10.2, 9.8, 10.5, 10.1, 9.9)

# Estimate parameters
fit <- util_normal_param_estimate(observed)

# Get estimates
fit$parameter_tbl
#> # A tibble: 2 × 8
#>   dist_type samp_size   min   max method              mu stan_dev shape_ratio
#>   <chr>         <int> <dbl> <dbl> <chr>            <dbl>    <dbl>       <dbl>
#> 1 Gaussian          5   9.8  10.5 EnvStats_MME_MLE  10.1    0.245        41.2
#> 2 Gaussian          5   9.8  10.5 EnvStats_MVUE     10.1    0.274        36.9

Estimation Methods

Maximum Likelihood Estimation (MLE)

Concept: Find parameters that maximize probability of observing the data

Characteristics: - Asymptotically efficient - Best for large samples (n > 30) - Most commonly used

Method of Moments Estimation (MME)

Concept: Match sample moments to theoretical moments

Characteristics: - Simpler computation - Often same as MLE for common distributions - Intuitive approach

Minimum Variance Unbiased Estimation (MVUE)

Concept: Unbiased estimates with minimum variance

Characteristics: - Best for small samples - Corrects for small-sample bias - Theoretically optimal when available

Model Selection

Akaike Information Criterion (AIC): - Balances fit quality with model complexity - Lower AIC = better model - Used to compare distributions

# Generate some data with local seed
data_y <- withr::with_seed(42, rnorm(100, mean = 5, sd = 2))

# Compare multiple distributions
normal_aic <- util_normal_aic(.x = data_y)
cauchy_aic <- util_cauchy_aic(.x = data_y)
logistic_aic <- util_logistic_aic(.x = data_y)

# Show AIC values
cat("Normal AIC:", normal_aic, "\n")
#> Normal AIC: 433.517
cat("Cauchy AIC:", cauchy_aic, "\n")
#> Cauchy AIC: 466.3125
cat("Logistic AIC:", logistic_aic, "\n")
#> Logistic AIC: 433.9747

# Choose distribution with lowest AIC
best_model <- c("Normal", "Cauchy", "Logistic")[which.min(c(normal_aic, cauchy_aic, logistic_aic))]
cat("Best model:", best_model, "\n")
#> Best model: Normal

Statistical Inference

Hypothesis Testing

Using distributions for hypothesis tests:

# Test if sample mean differs from 0
observed_data <- withr::with_seed(456, rnorm(100, mean = 0.5, sd = 1))

# Generate null distribution with local seed
null_dist <- withr::with_seed(789, tidy_normal(.n = 100, .mean = 0, .sd = 1, .num_sims = 1000))

# Calculate test statistic
observed_mean <- mean(observed_data)

# Calculate null means for each simulation
null_means <- null_dist |>
  group_by(sim_number) |>
  summarise(sim_mean = mean(y), .groups = "drop")

# P-value: proportion of null means more extreme than observed
p_value <- mean(abs(null_means$sim_mean) >= abs(observed_mean))
cat("The mean of observed data is:", observed_mean, "\n")
#> The mean of observed data is: 0.6205748
cat("The p-value is:", p_value, "\n")
#> The p-value is: 0

Confidence Intervals

Bootstrap confidence intervals:

# Bootstrap resampling
boot_data <- tidy_bootstrap(.x = observed_data, .num_sims = 2000)

# Calculate 95% CI
ci <- boot_data |>
  bootstrap_unnest_tbl() |>
  summarise(
    lower = quantile(y, 0.025),
    upper = quantile(y, 0.975)
  )

cat("95% Confidence Interval:", ci$lower, "to", ci$upper, "\n")
#> 95% Confidence Interval: -1.22054 to 2.520635

Power Analysis

Determining required sample size:

# Simulate to estimate power
simulate_test <- function(n, effect_size, alpha = 0.05) {
  group1 <- rnorm(n, mean = 0, sd = 1)
  group2 <- rnorm(n, mean = effect_size, sd = 1)
  t.test(group1, group2)$p.value < alpha
}

# Run many simulations
n_sims <- 1000
power <- mean(replicate(n_sims, simulate_test(n = 50, effect_size = 0.5)))
cat("Power:", power, "\n")
#> Power: 0.68

Tidyverse Integration

Works with dplyr

tidy_normal(.n = 100, .num_sims = 5) |>
  group_by(sim_number) |>
  summarise(
    mean = mean(y),
    sd = sd(y),
    median = median(y)
  ) |>
  arrange(desc(mean))
#> # A tibble: 5 × 4
#>   sim_number   mean    sd  median
#>   <fct>       <dbl> <dbl>   <dbl>
#> 1 4          0.196  1.01   0.208 
#> 2 2          0.107  0.986  0.0464
#> 3 3          0.0651 1.01  -0.0146
#> 4 1          0.0201 0.986 -0.0117
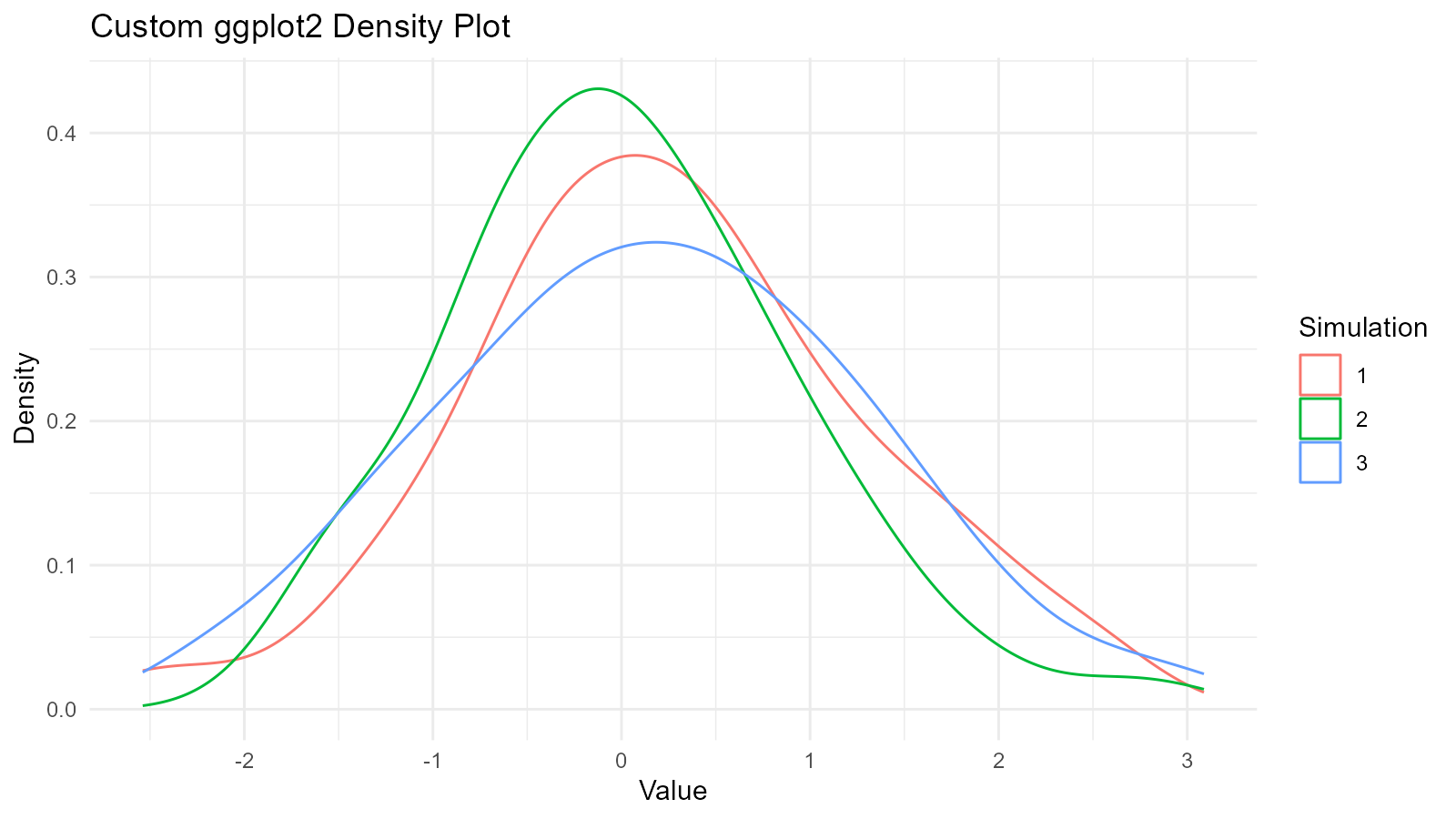
#> 5 5          0.0125 1.08  -0.109

Works with ggplot2

data <- tidy_normal(.n = 100, .num_sims = 3)

# Custom ggplot
ggplot(data, aes(x = y, color = sim_number)) +
  geom_density() +
  theme_minimal() +
  labs(
    title = "Custom ggplot2 Density Plot",
    x = "Value",
    y = "Density",
    color = "Simulation"
  )

Works with tidyr

library(tidyr)

data <- tidy_normal(.n = 100, .num_sims = 3)

# Widen data
wide_data <- data |>
  select(sim_number, x, y) |>
  pivot_wider(names_from = sim_number, values_from = y, names_prefix = "sim_")

head(wide_data)
#> # A tibble: 6 × 4
#>       x  sim_1  sim_2  sim_3
#>   <int>  <dbl>  <dbl>  <dbl>
#> 1     1 -1.73  -1.76   0.191
#> 2     2  1.34   1.73   1.14 
#> 3     3  2.07  -0.213  1.55 
#> 4     4 -0.546  0.902  0.701
#> 5     5 -0.628 -0.426  1.02 
#> 6     6  0.254  0.855 -1.74

Works with purrr

library(purrr)

# Generate multiple distributions
distributions <- list(
  normal = tidy_normal(.n = 100),
  gamma = tidy_gamma(.n = 100, .shape = 2, .scale = 1),
  beta = tidy_beta(.n = 100, .shape1 = 2, .shape2 = 5)
)

# Map over distributions
distributions |>
  map(~ summarise(., mean = mean(y), sd = sd(y)))
#> $normal
#> # A tibble: 1 × 2
#>     mean    sd
#>    <dbl> <dbl>
#> 1 0.0931 0.902
#> 
#> $gamma
#> # A tibble: 1 × 2
#>    mean    sd
#>   <dbl> <dbl>
#> 1  1.87  1.31
#> 
#> $beta
#> # A tibble: 1 × 2
#>    mean    sd
#>   <dbl> <dbl>
#> 1 0.274 0.152

Key Takeaways

1. Tidy Format Enables Analysis

Every TidyDensity function returns a structured tibble that works with tidyverse tools.

2. Four Functions (d, p, q, r)

Understanding these four functions is key to working with distributions.

3. Multiple Methods Available

Use MLE for large samples, MVUE for small samples, compare with AIC.

4. Reproducibility Matters

Use withr::with_seed() for reproducible random number generation with explicit scope.

5. Visualization is Essential

Always plot your data and fitted distributions to validate assumptions.