Skip to contents

Advanced Features

Source: vignettes/advanced-features.Rmd
advanced-features.Rmd

TidyDensity offers powerful advanced features including mixture models, empirical distributions, random walks, and multi-distribution comparisons.

Mixture Models

What are Mixture Models?

Mixture models combine multiple probability distributions to model complex data patterns:

  • Multimodal distributions (multiple peaks)
  • Heterogeneous populations
  • Complex real-world phenomena

Creating Mixture Models

Basic Mixture Creation 

dist1 <- tidy_normal(.n = 100, .mean = -2, .sd = 0.5)
dist2 <- tidy_normal(.n = 100, .mean = 2, .sd = 0.5)

# Create mixture
mixture <- tidy_mixture_density(
  dist1,
  dist2,
  .combination_type = "stack"
)

# Visualize
mixture$plots
#> $line_plot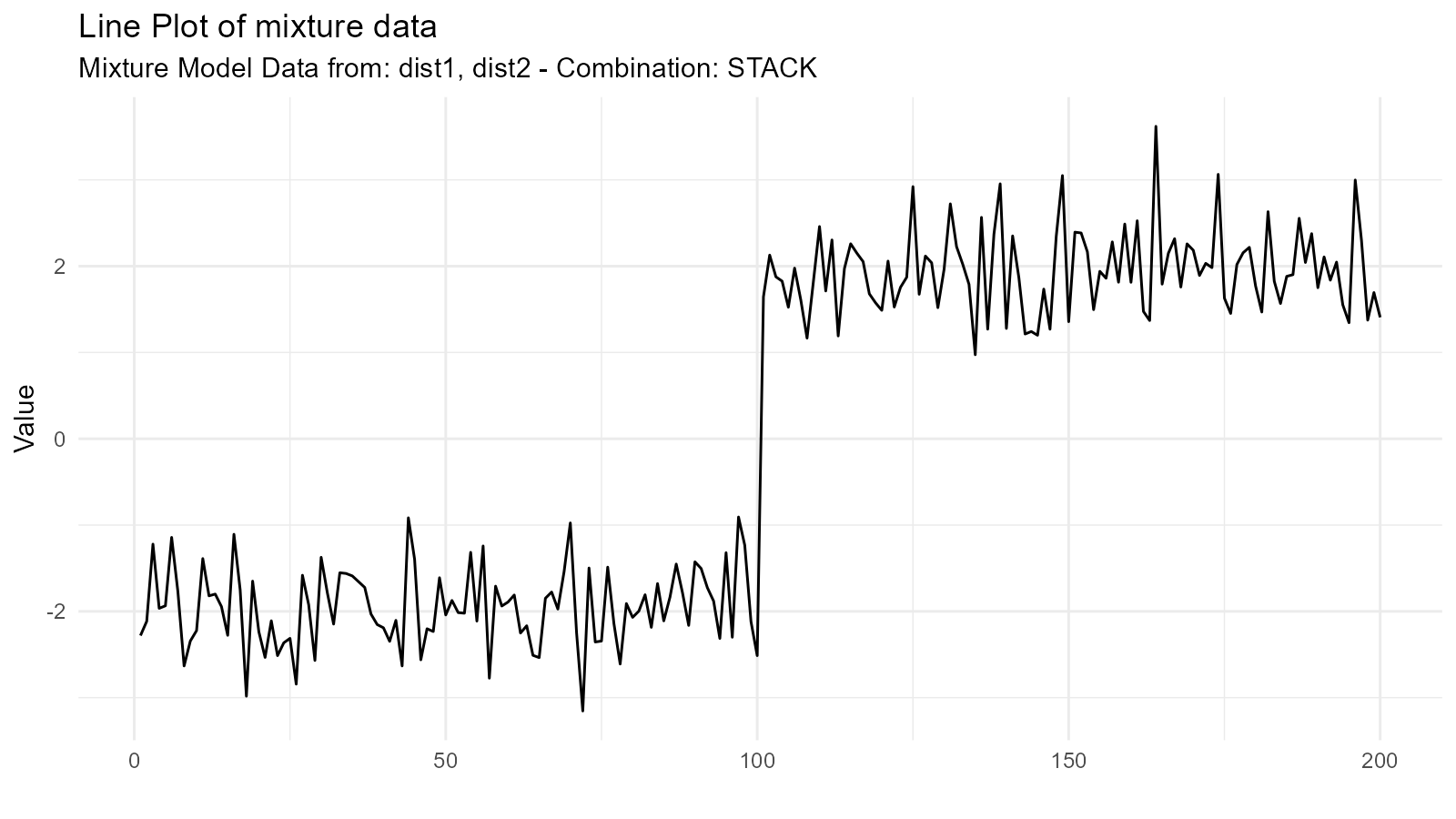

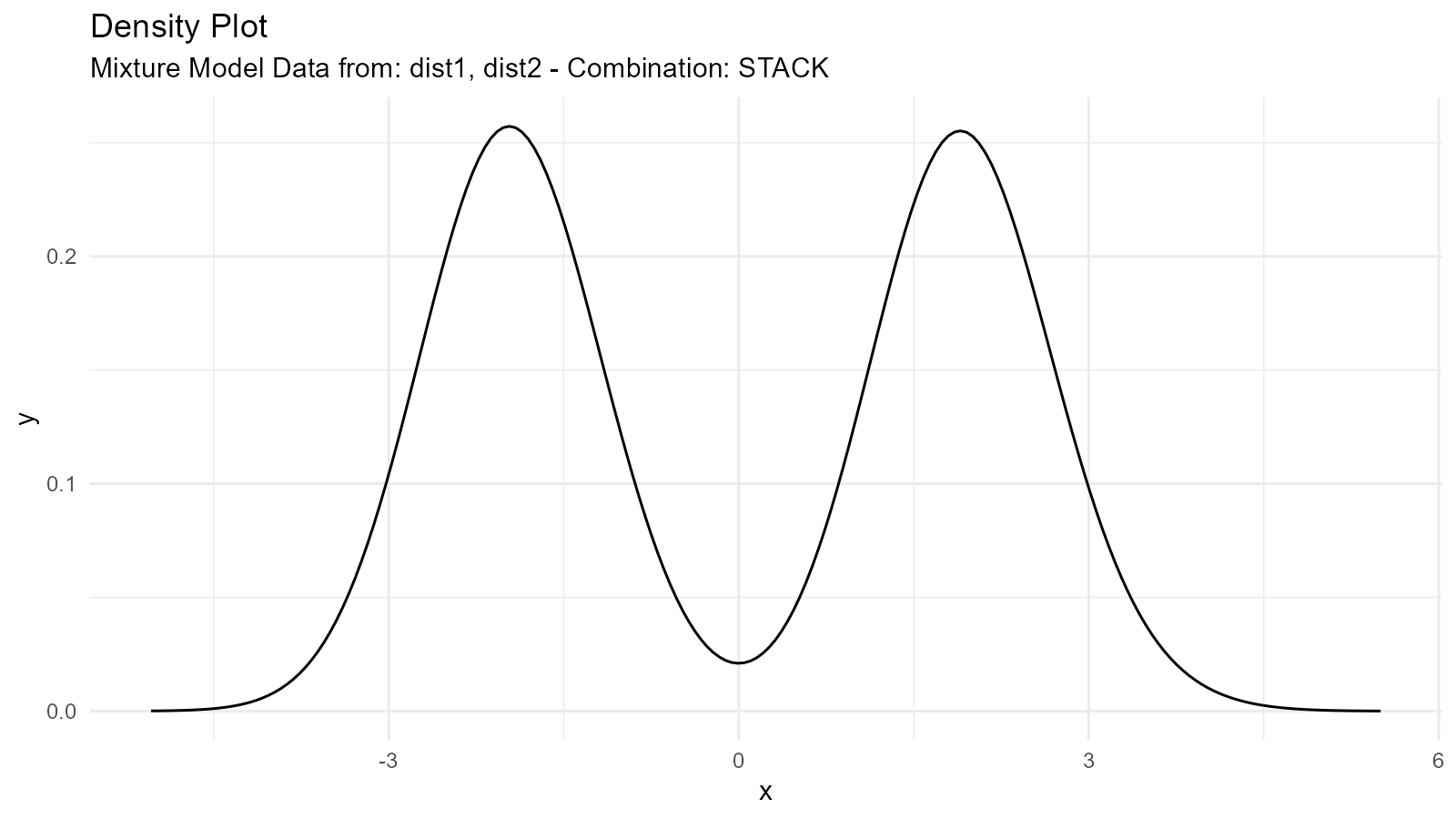
Density plot of a bimodal mixture distribution created by combining two normal distributions centered at -2 and 2

#> 
#> $dens_plot

Density plot of a bimodal mixture distribution created by combining two normal distributions centered at -2 and 2

Mixture Types

1. Addition Mixture ("add")

Combines distributions by adding their sample values (element-wise) and then computing the resulting density:

mixture_add <- tidy_mixture_density(
  dist1, dist2,
  .combination_type = "add"
)

mixture_add$plots
#> $line_plot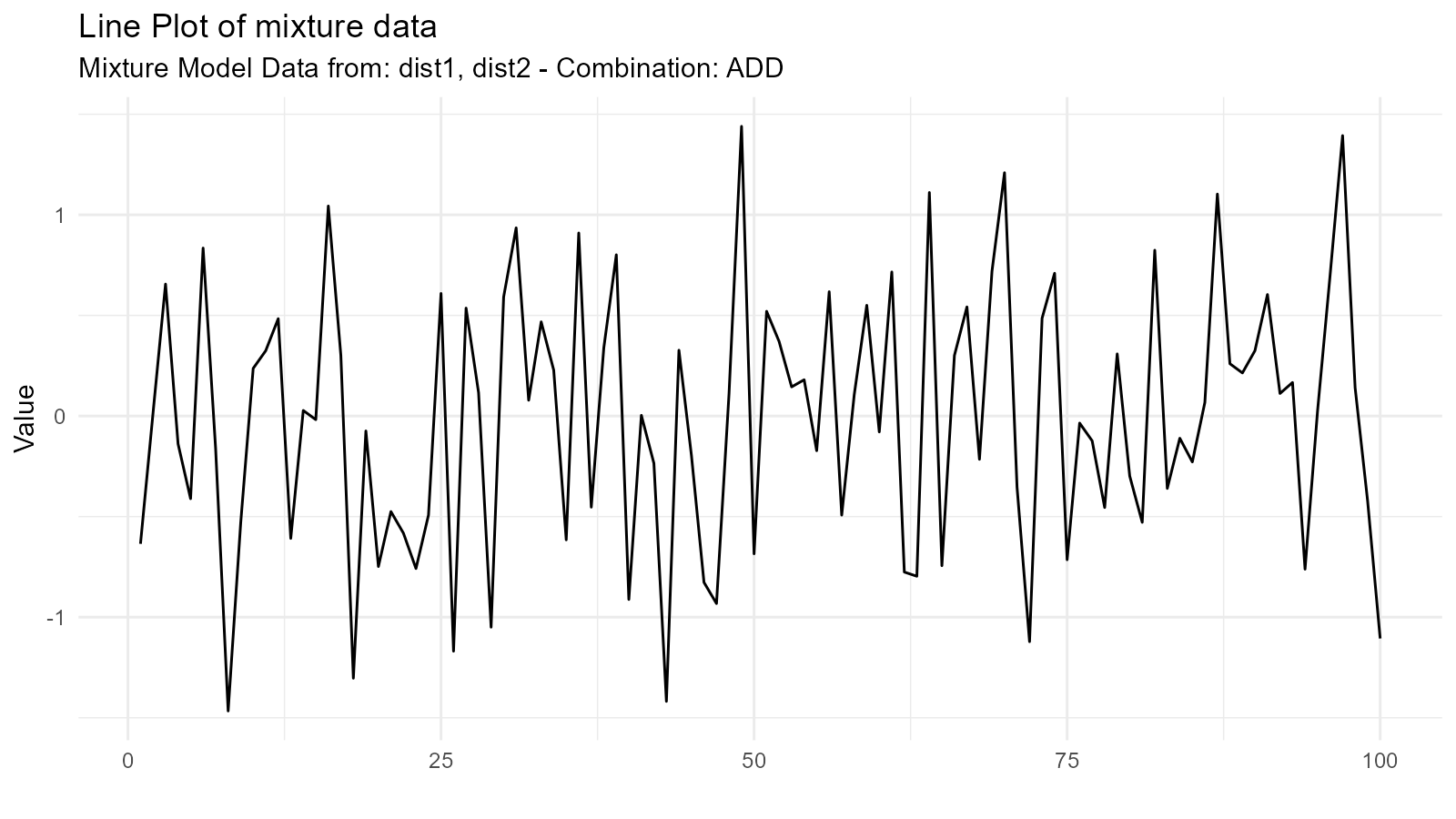

Density plot showing an addition mixture of two normal distributions, creating a bimodal pattern with peaks at -2 and 2

#> 
#> $dens_plot

Density plot showing an addition mixture of two normal distributions, creating a bimodal pattern with peaks at -2 and 2

Use Case: Modeling populations with two distinct groups

2. Multiplication Mixture ("multiply")

Multiplies distributions:

mixture_mult <- tidy_mixture_density(
  dist1, dist2,
  .combination_type = "multiply"
)

mixture_mult$plots
#> $line_plot

Density plot showing a multiplication mixture of two normal distributions, resulting in a peaked distribution where both source distributions overlap

#> 
#> $dens_plot

Density plot showing a multiplication mixture of two normal distributions, resulting in a peaked distribution where both source distributions overlap

Use Case: Modeling joint effects or constraints

3. Subtraction Mixture ("subtract")

Subtracts second from first:

mixture_sub <- tidy_mixture_density(
  dist1, dist2,
  .combination_type = "subtract"
)

mixture_sub$plots
#> $line_plot

Density plot showing a subtraction mixture where the second normal distribution is subtracted from the first

#> 
#> $dens_plot

Density plot showing a subtraction mixture where the second normal distribution is subtracted from the first

Use Case: Modeling differences between groups

4. Division Mixture ("divide")

Divides first by second:

mixture_div <- tidy_mixture_density(
  dist1, dist2,
  .combination_type = "divide"
)

mixture_div$plots
#> $line_plot

Density plot showing a division mixture where the first normal distribution is divided by the second

#> 
#> $dens_plot

Density plot showing a division mixture where the first normal distribution is divided by the second

Use Case: Ratios of distributions

Complex Mixture Example 

# Three-component mixture
dist_a <- tidy_normal(.n = 100, .mean = -3, .sd = 0.5)
dist_b <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
dist_c <- tidy_normal(.n = 100, .mean = 3, .sd = 0.5)

# Create mixture
complex_mixture <- tidy_mixture_density(
  dist_a, dist_b, dist_c,
  .combination_type = "stack"
)

# Visualize
complex_mixture$plots
#> $line_plot

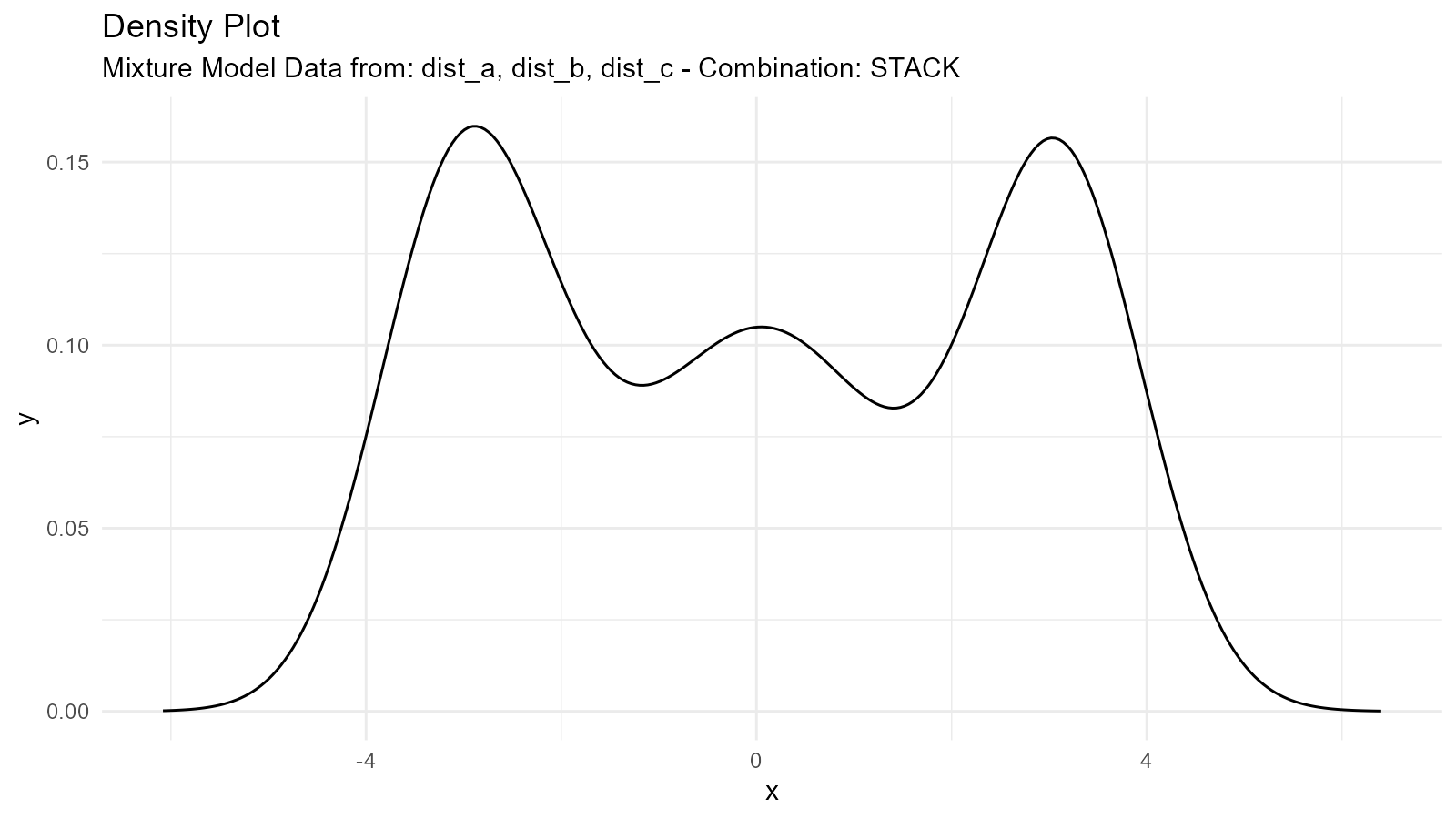
Density plot of a three-component mixture model combining normal distributions centered at -3, 0, and 3, creating a trimodal pattern

#> 
#> $dens_plot

Density plot of a three-component mixture model combining normal distributions centered at -3, 0, and 3, creating a trimodal pattern

Weighted Mixtures

Create weighted combinations by adjusting the .n parameter:

# Generate components
dist_heavy <- tidy_normal(.n = 300, .mean = -2, .sd = 0.5)  # 75% weight
dist_light <- tidy_normal(.n = 100, .mean = 2, .sd = 0.5)   # 25% weight

# Scale densities by intended weights
dist_heavy_weighted <- dplyr::mutate(dist_heavy, y = 0.75 * y)
dist_light_weighted <- dplyr::mutate(dist_light, y = 0.25 * y)

# Create weighted mixture
weighted_mixture <- tidy_mixture_density(
  dist_heavy_weighted, dist_light_weighted,
  .combination_type = "stack"
)

weighted_mixture$plots
#> $line_plot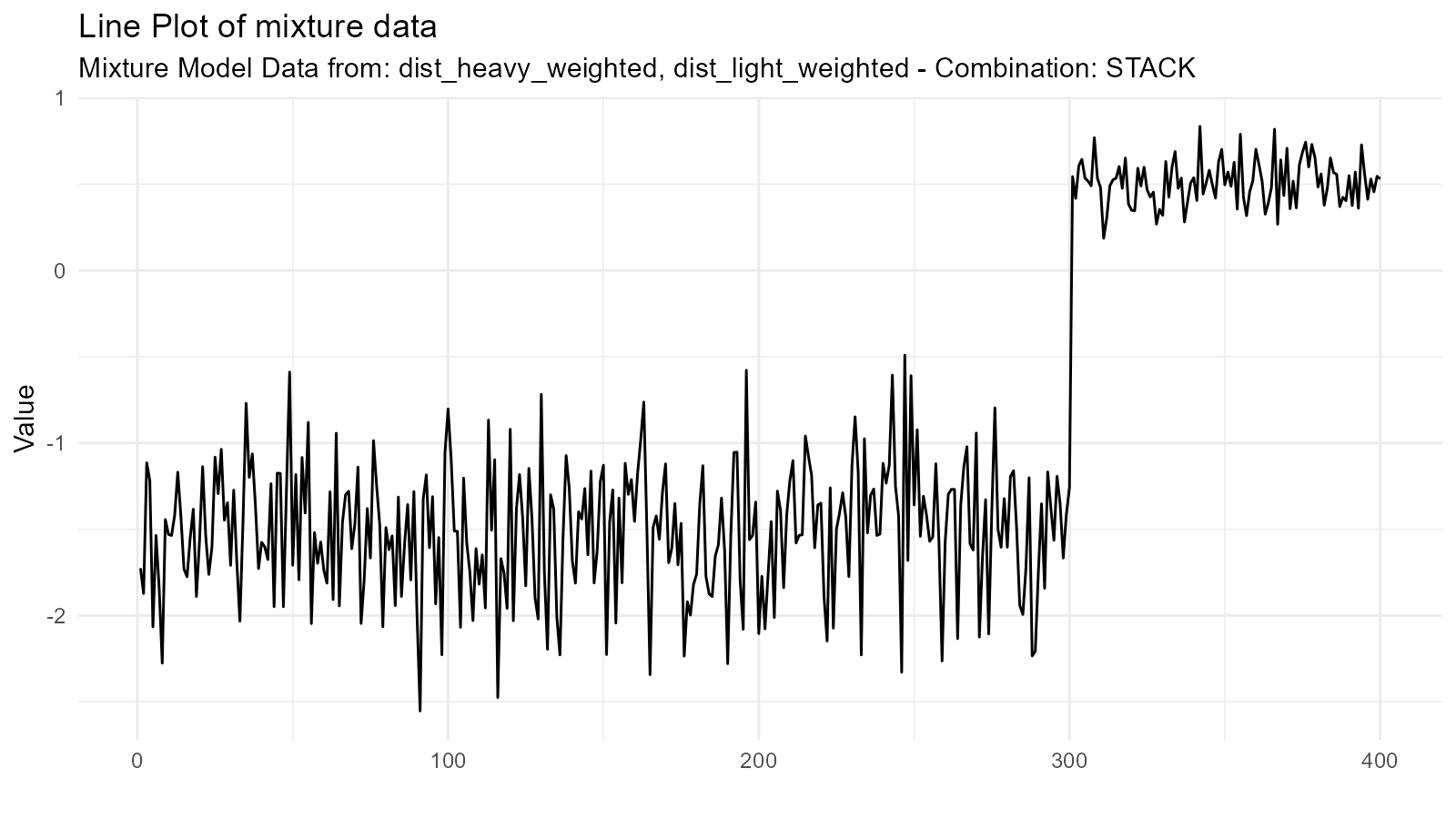

Density p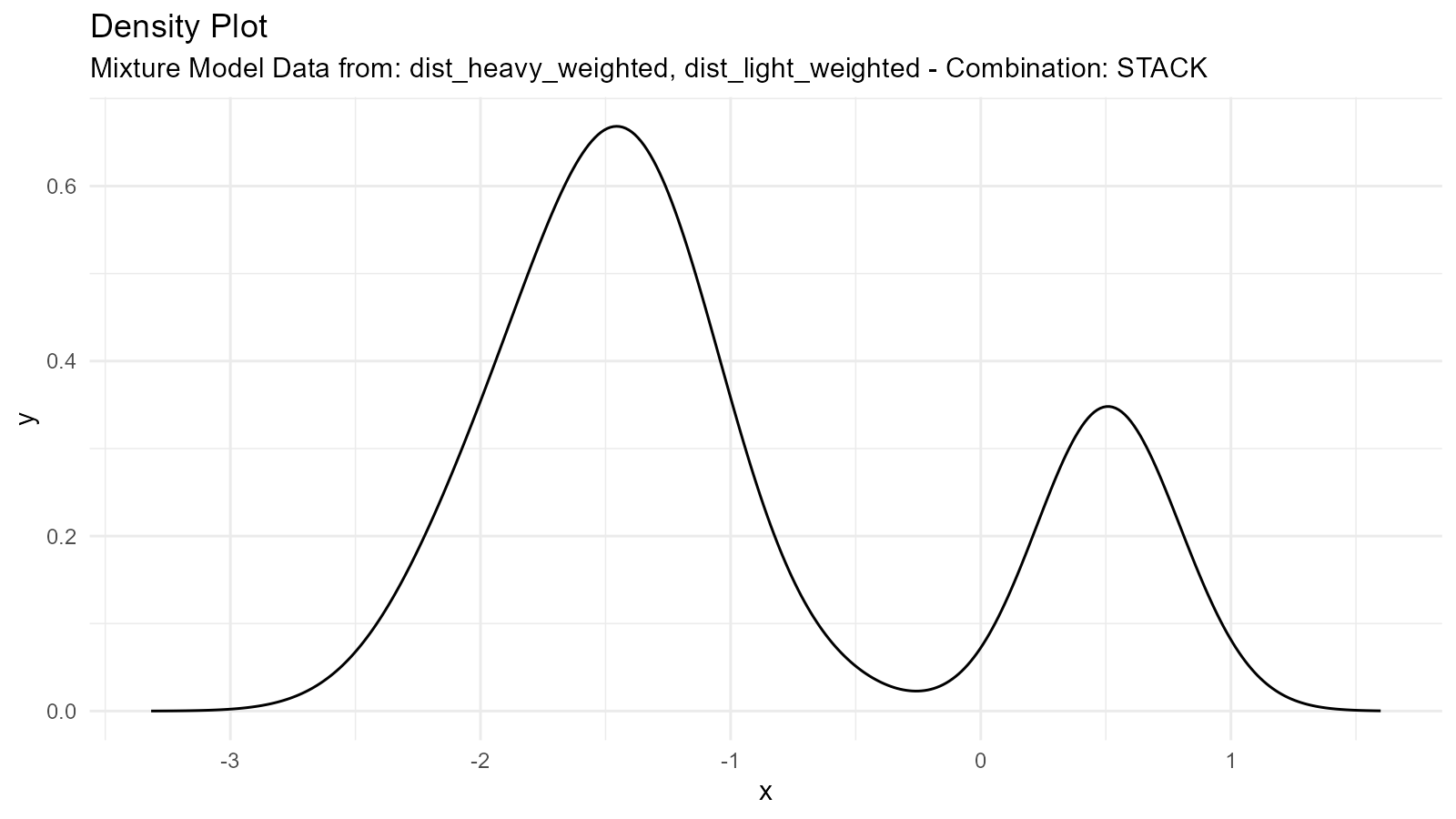lot of a weighted bimodal mixture where the left peak at -2 is more prominent (75% weight) than the right peak at 2 (25% weight)

#> 
#> $dens_plot

Density plot of a weighted bimodal mixture where the left peak at -2 is more prominent (75% weight) than the right peak at 2 (25% weight)

Different Distribution Types

Mix different distribution families:

# Mix normal and gamma
normal <- tidy_normal(.n = 100, .mean = 5, .sd = 1)
gamma <- tidy_gamma(.n = 100, .shape = 2, .scale = 2)

# Create mixture
mixed_family <- tidy_mixture_density(
  normal, gamma,
  .combination_type = "stack"
)

mixed_family$plots
#> $line_plot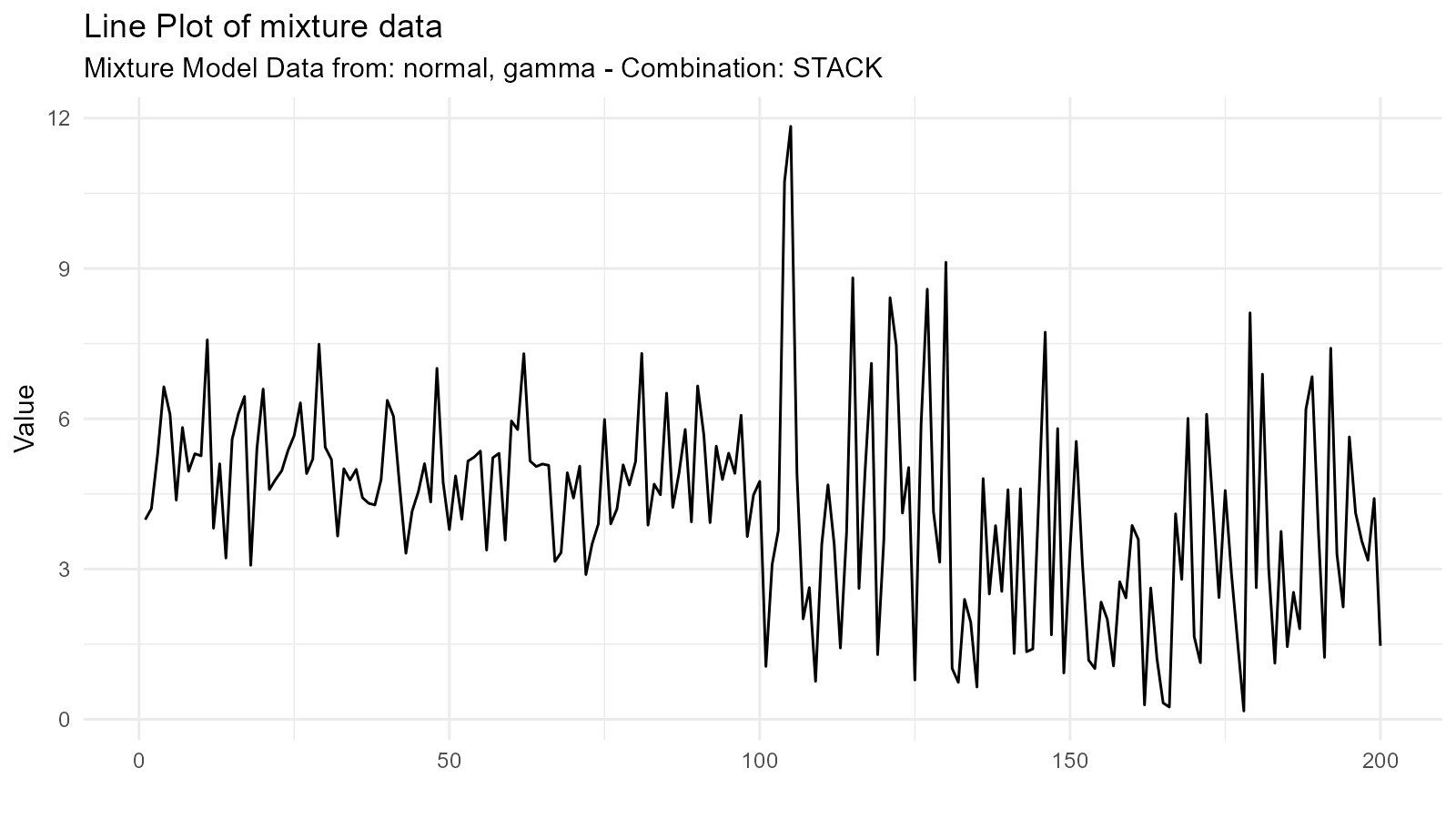

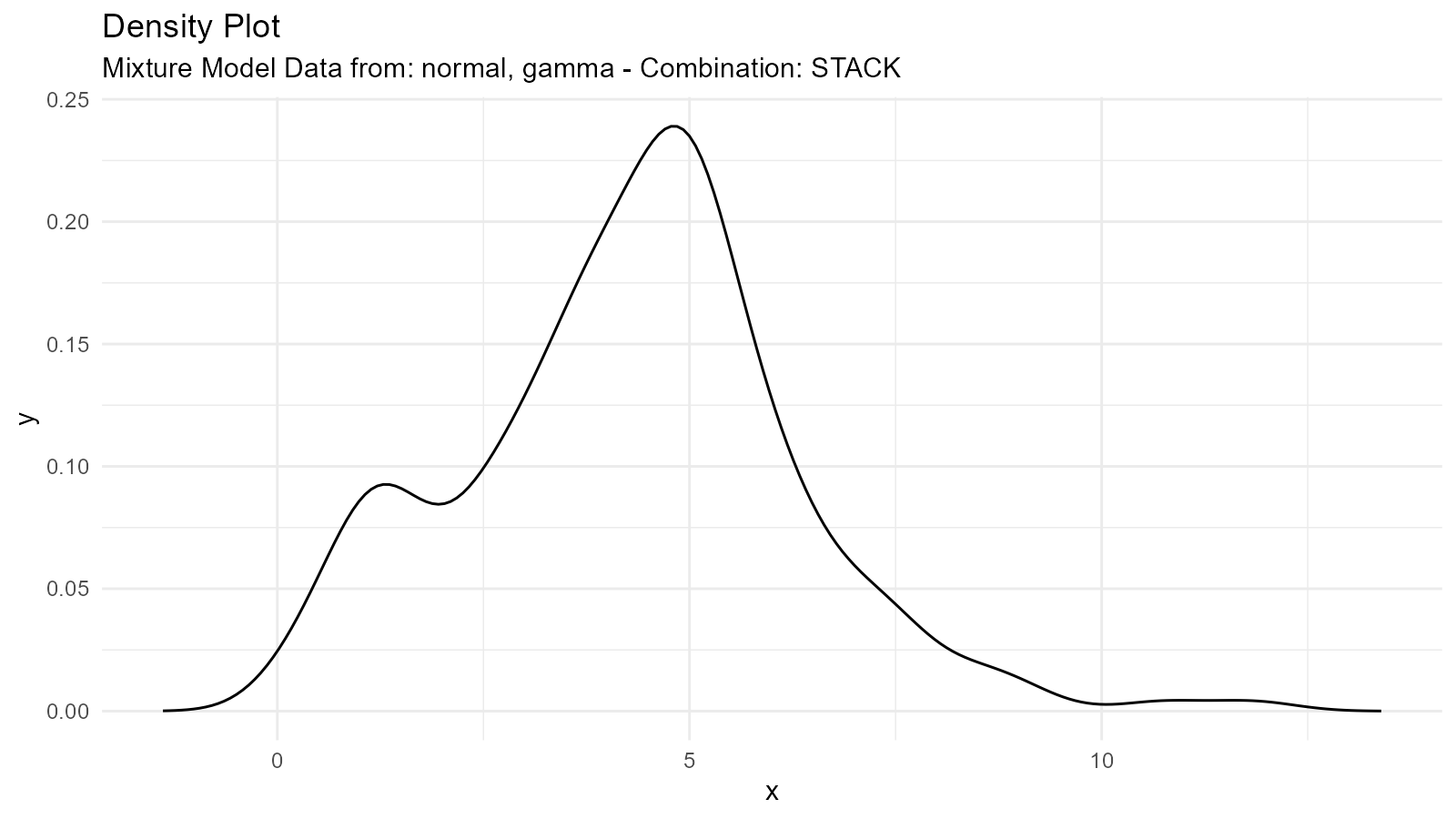
Density plot of a mixture combining a normal distribution centered at 5 with a gamma distribution, showing how different distribution families can be combined

#> 
#> $dens_plot

Density plot of a mixture combining a normal distribution centered at 5 with a gamma distribution, showing how different distribution families can be combined

Empirical Distributions

What are Empirical Distributions?

Work directly with your observed data without assuming a distribution:

# Your observed data
observed_data <- mtcars$mpg

# Create empirical distribution
empirical <- tidy_empirical(
  .x = observed_data,
  .num_sims = 1
)

# Visualize
tidy_autoplot(empirical, .plot_type = "density")

Density plot of an empirical distribution created from the mtcars mpg data, showing the observed data distribution

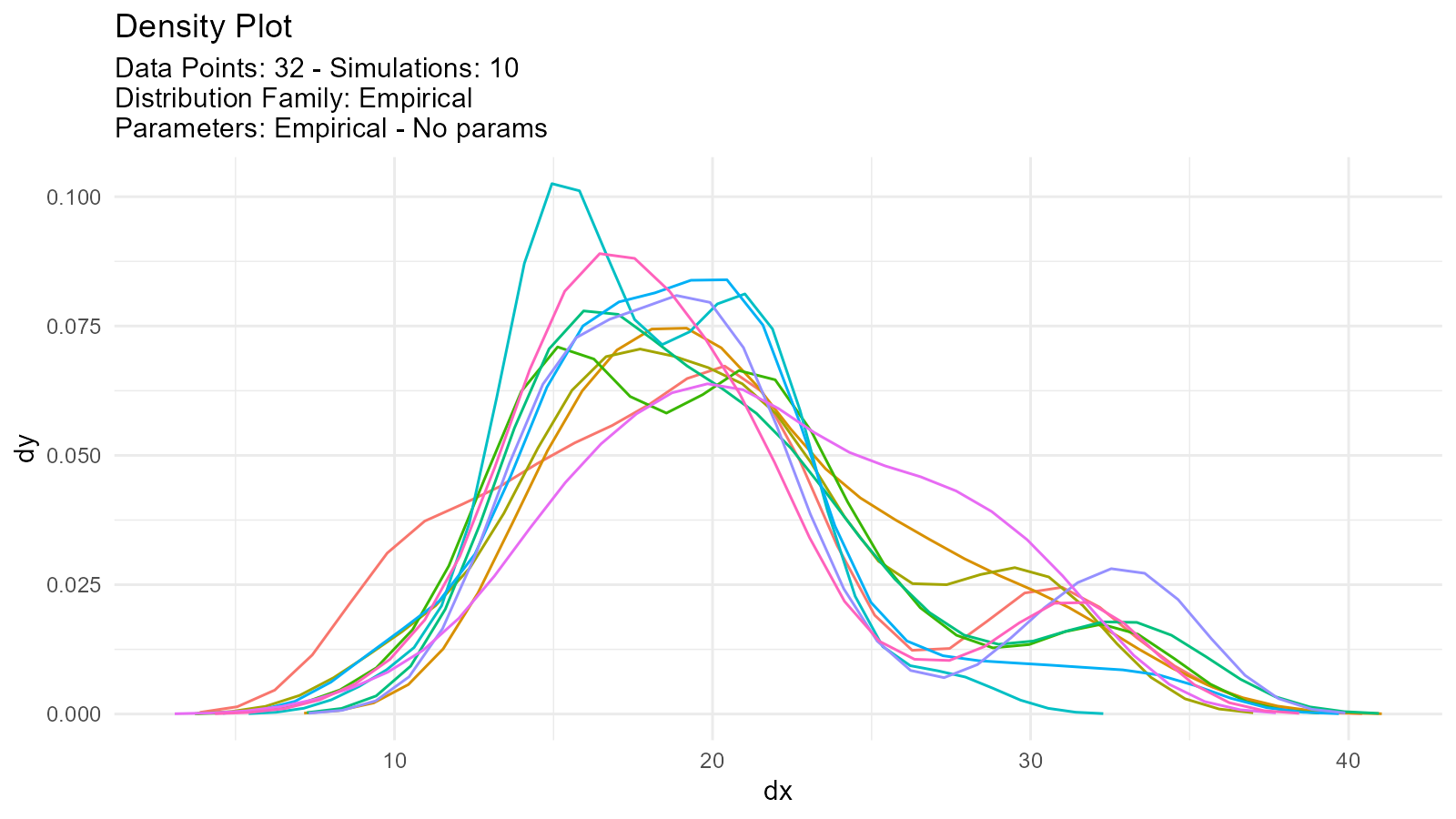
Multiple Empirical Simulations

Generate multiple resamples:

# Multiple bootstrap-like samples
empirical_multi <- tidy_empirical(
  .x = observed_data,
  .num_sims = 5
)

tidy_autoplot(empirical_multi, .plot_type = "density")

Density plot showing 5 bootstrap-like resamples of the mtcars mpg data, with each simulation shown in a different color

Comparing Empirical with Theoretical 

# Observed data
data <- mtcars$mpg

# Empirical distribution
empirical <- tidy_empirical(.x = data, .num_sims = 1)

# Fitted theoretical distribution
theoretical <- tidy_normal(
  .n = length(data),
  .mean = mean(data),
  .sd = sd(data)
)

# Combine for comparison
combined <- tidy_combine_distributions(empirical, theoretical)

# Plot
tidy_combined_autoplot(combined)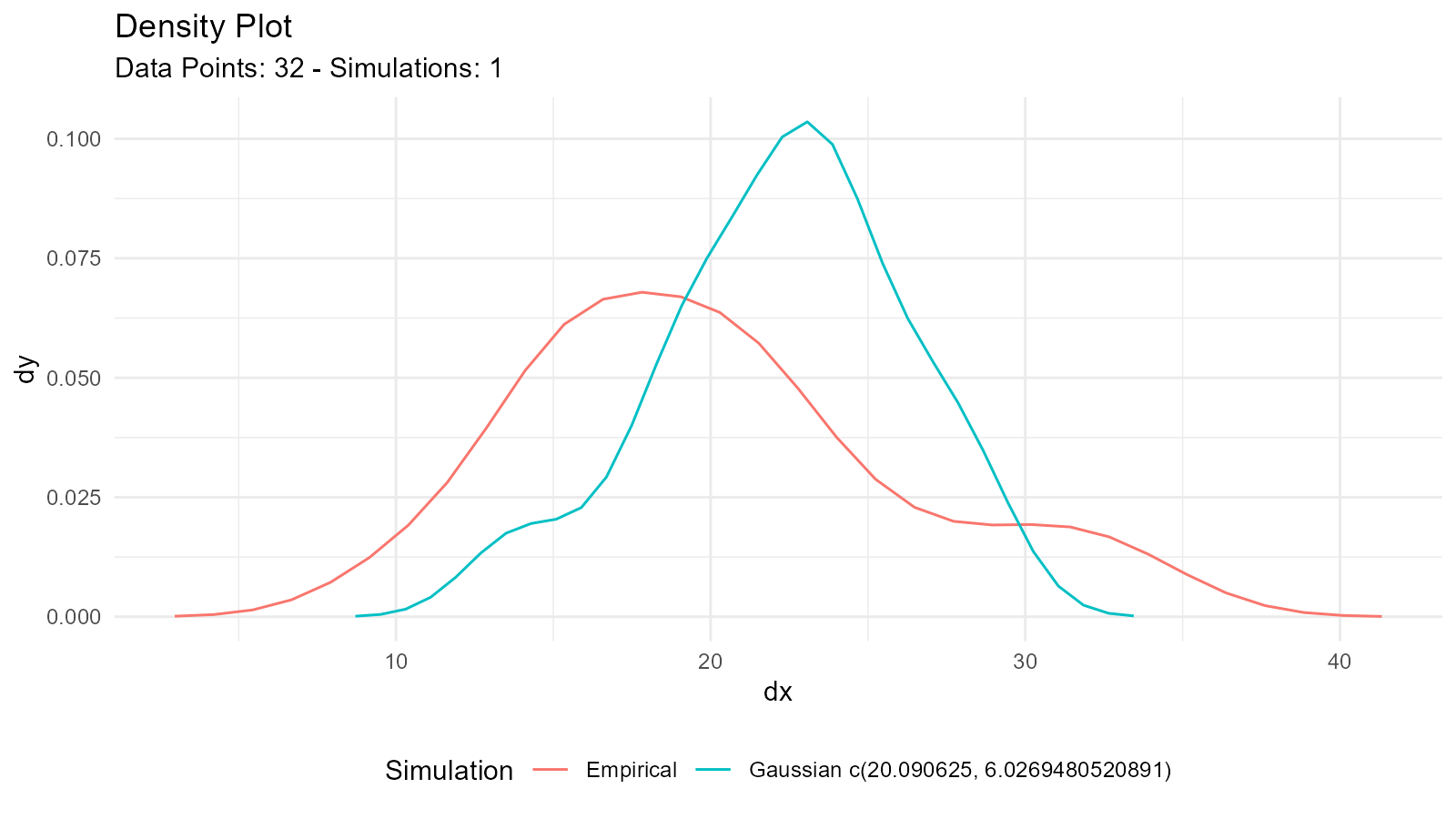

Combined density plot comparing the empirical distribution of mtcars mpg data with a fitted normal distribution, allowing visual assessment of fit

Empirical Bootstrap

Combine empirical with bootstrap:

# Bootstrap from empirical data
boot_empirical <- tidy_bootstrap(
  .x = observed_data,
  .num_sims = 100
)

# Visualize bootstrap distribution
bootstrap_stat_plot(boot_empirical, .value = y, .stat = "cmean")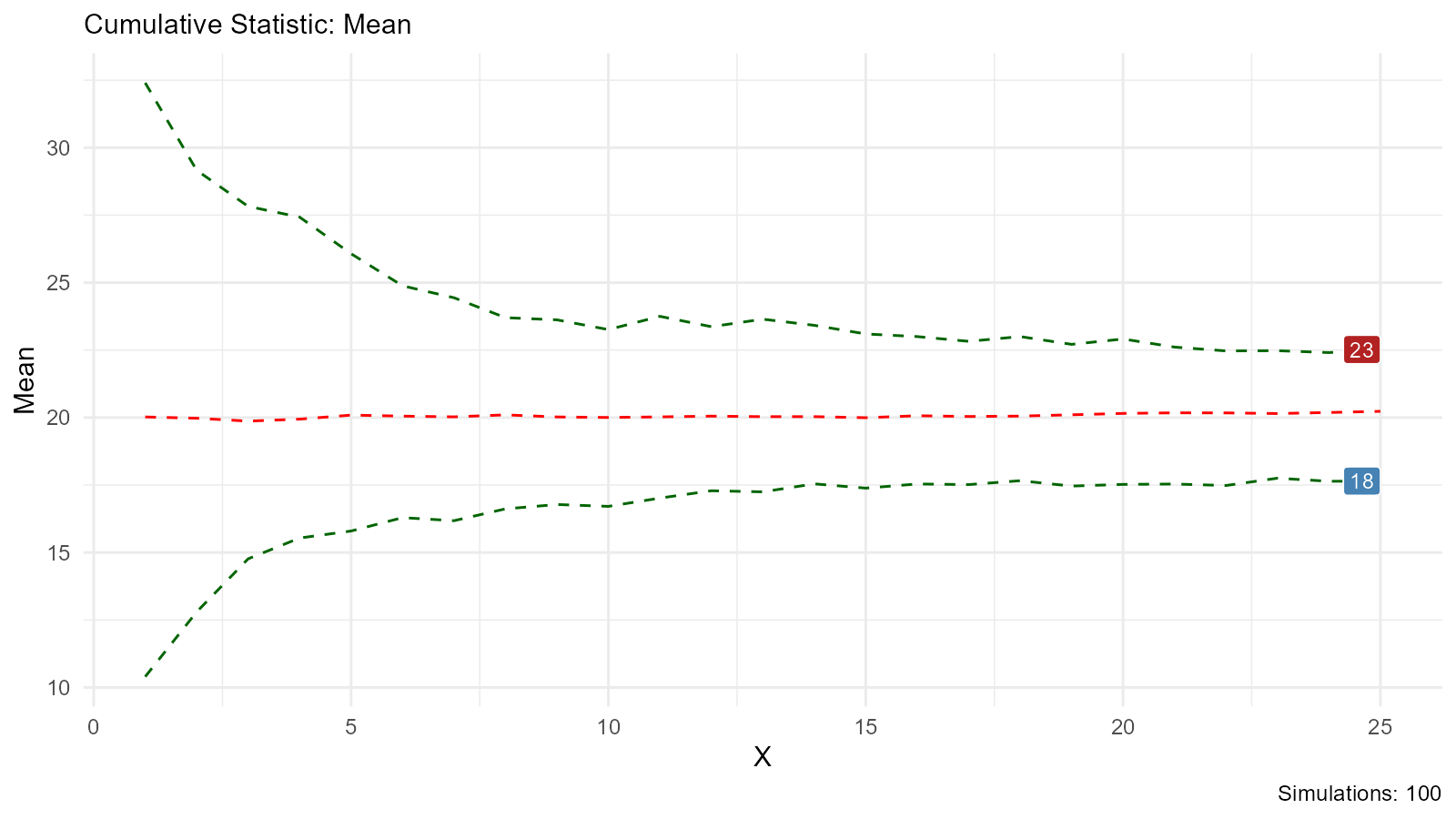

Plot showing bootstrap resamples of the observed data with cumulative mean statistic, demonstrating convergence behavior

Multi-Distribution Comparison

Compare Same Distribution with Different Parameters 

# Compare normal distributions with different parameters
comparison <- tidy_multi_single_dist(
  .tidy_dist = "tidy_normal",
  .param_list = list(
    .n = 100,
    .mean = c(-2, 0, 2),
    .sd = 1,
    .num_sims = 5,
    .return_tibble = TRUE
  )
)

# Visualize
tidy_multi_dist_autoplot(comparison)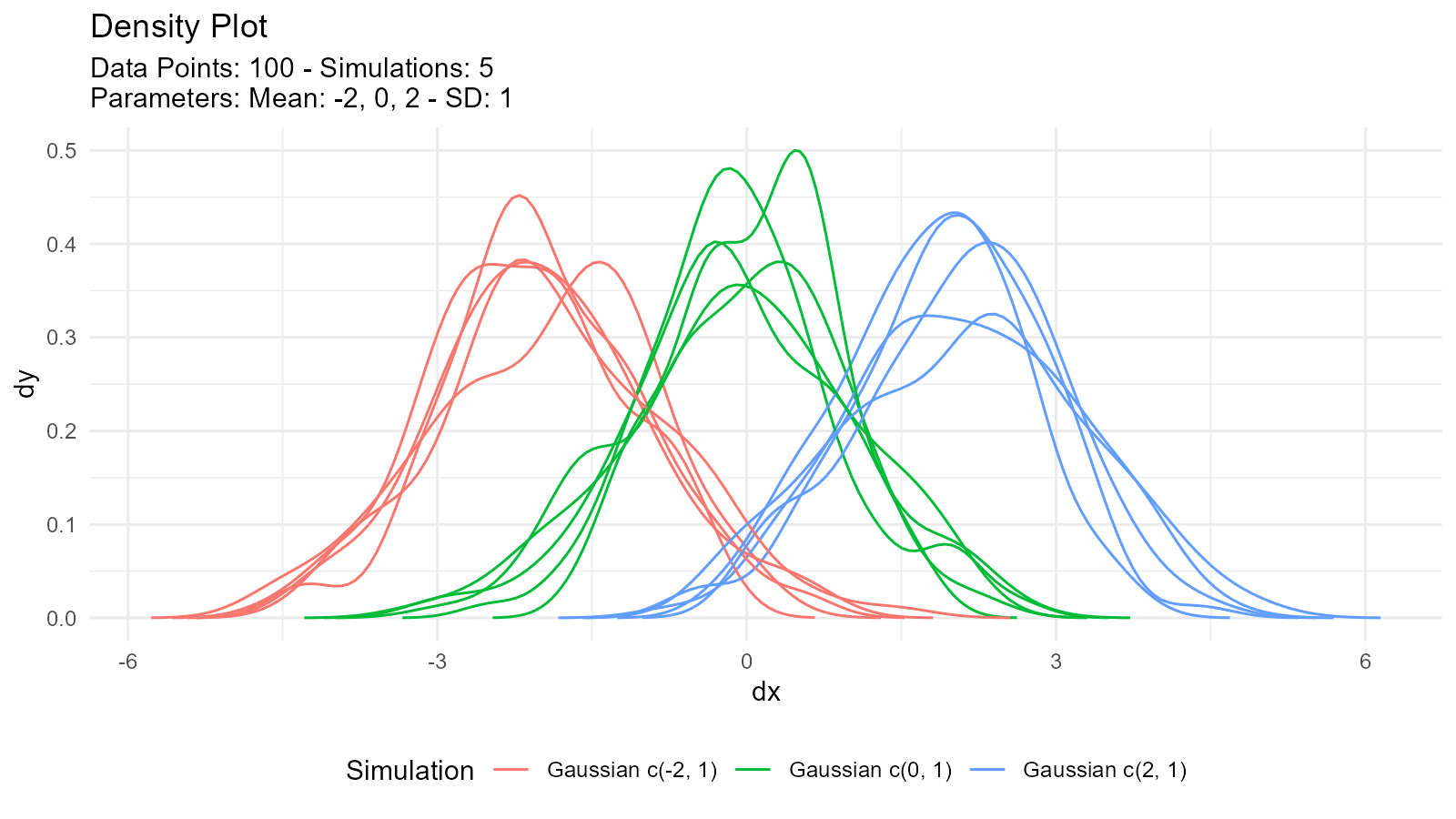

Density plot comparing three normal distributions with means at -2, 0, and 2, showing how changing parameters affects the distribution shape and location

Compare Different Distributions 

# Generate different distributions
normal <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
cauchy <- tidy_cauchy(.n = 100, .location = 0, .scale = 1)
logistic <- tidy_logistic(.n = 100, .location = 0, .scale = 1)

# Combine
combined <- tidy_combine_distributions(normal, cauchy, logistic)

# Visualize
tidy_combined_autoplot(combined)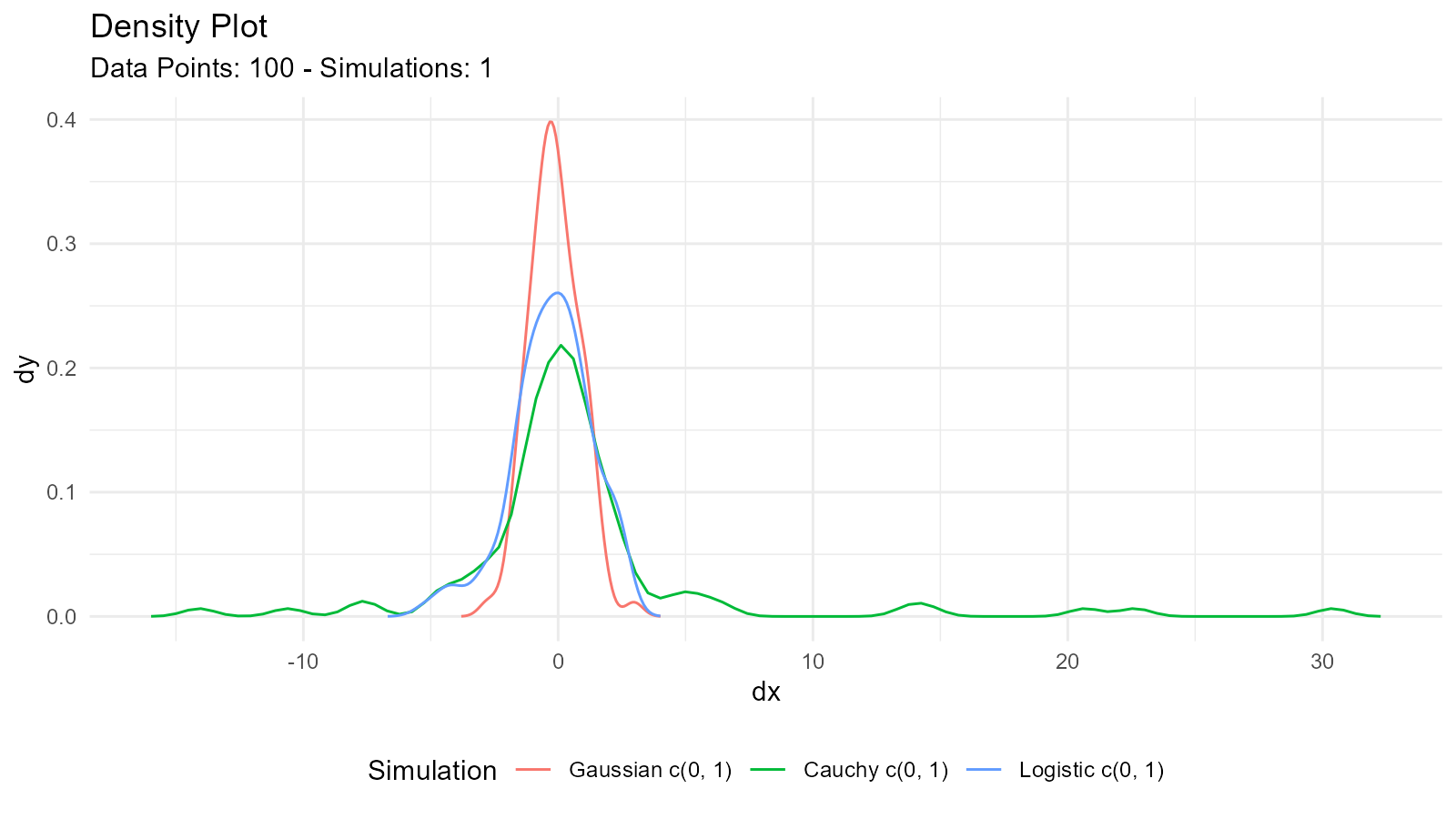

Combined density plot comparing normal, Cauchy, and logistic distributions with matching location and scale parameters, highlighting their different tail behaviors

Random Walk Generation

Basic Random Walk 

# Generate random walk
rw <- tidy_normal(.sd = .1, .num_sims = 25) |>
  tidy_random_walk(.value_type = "cum_sum")

head(rw)
#> # A tibble: 6 × 8
#>   sim_number     x        y     dx      dy     p        q random_walk_value
#>   <fct>      <int>    <dbl>  <dbl>   <dbl> <dbl>    <dbl>             <dbl>
#> 1 1              1 -0.0637  -0.400 0.00242 0.262 -0.0637            -0.0637
#> 2 1              2  0.00175 -0.384 0.00762 0.507  0.00175           -0.0619
#> 3 1              3  0.130   -0.369 0.0204  0.903  0.130              0.0680
#> 4 1              4 -0.0794  -0.354 0.0463  0.214 -0.0794            -0.0113
#> 5 1              5 -0.0123  -0.339 0.0897  0.451 -0.0123            -0.0236
#> 6 1              6  0.00993 -0.324 0.149   0.540  0.00993           -0.0136

Random Walk Visualization 

ggplot(rw, aes(x = x, y = random_walk_value, color = sim_number, group = sim_number)) +
  geom_line() +
  labs(
    title = "Random Walk Simulations",
    x = "Step",
    y = "Cumulative Value",
    color = "Simulation"
  ) +
  theme_minimal() +
  theme(legend.position = "none")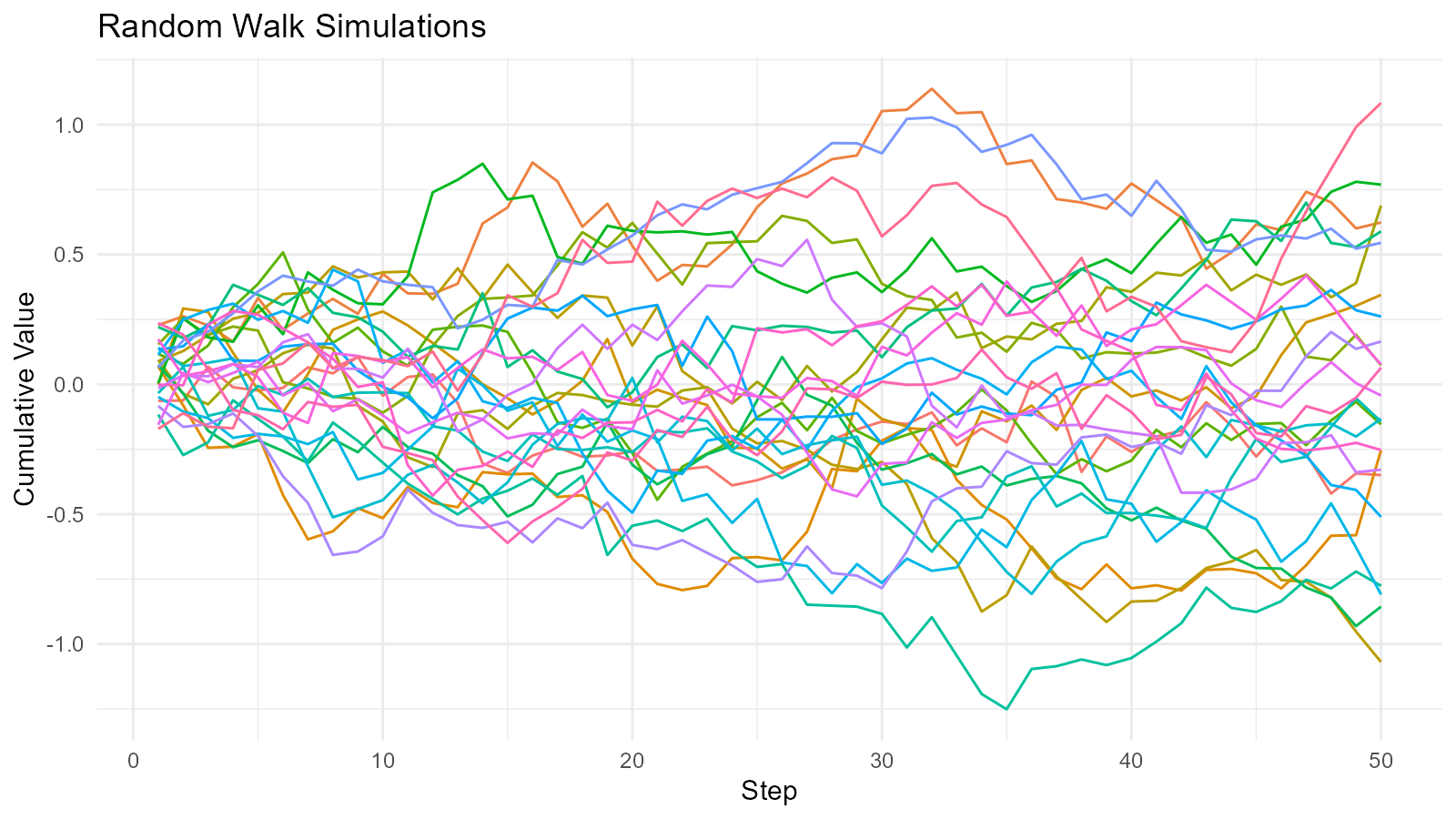

Line plot visualizing multiple random walk paths, with each simulation shown in a different color, illustrating the variability of random walks

Random Walk Analysis 

# Analyze random walk endpoints
rw_analysis <- rw |>
  group_by(sim_number) |>
  summarise(
    final_position = last(random_walk_value),
    max_position = max(random_walk_value),
    min_position = min(random_walk_value),
    range = max(random_walk_value) - min(random_walk_value)
  )

rw_analysis
#> # A tibble: 25 × 5
#>    sim_number final_position max_position min_position range
#>    <fct>               <dbl>        <dbl>        <dbl> <dbl>
#>  1 1                 -0.349        0.106      -0.421   0.527
#>  2 2                  0.623        1.14        0.164   0.974
#>  3 3                 -0.254        0.0686     -0.794   0.863
#>  4 4                  0.345        0.345      -0.400   0.745
#>  5 5                 -1.07         0.461      -1.07    1.53 
#>  6 6                  0.689        0.689      -0.319   1.01 
#>  7 7                  0.0732       0.649      -0.110   0.758
#>  8 8                 -0.154        0.508      -0.445   0.953
#>  9 9                  0.769        0.850       0.00377 0.846
#> 10 10                -0.856        0.106      -0.931   1.04 
#> # ℹ 15 more rows

Distribution Combinations

Combining Multiple Distributions 

# Create several distributions
dist_norm <- tidy_normal(.n = 100, .mean = 0, .sd = 1)
dist_gamma <- tidy_gamma(.n = 100, .shape = 2, .scale = 1)
dist_beta <- tidy_beta(.n = 100, .shape1 = 2, .shape2 = 5)

# Combine into one tibble
combined_dists <- tidy_combine_distributions(dist_norm, dist_gamma, dist_beta)

# Visualize all together
tidy_combined_autoplot(combined_dists)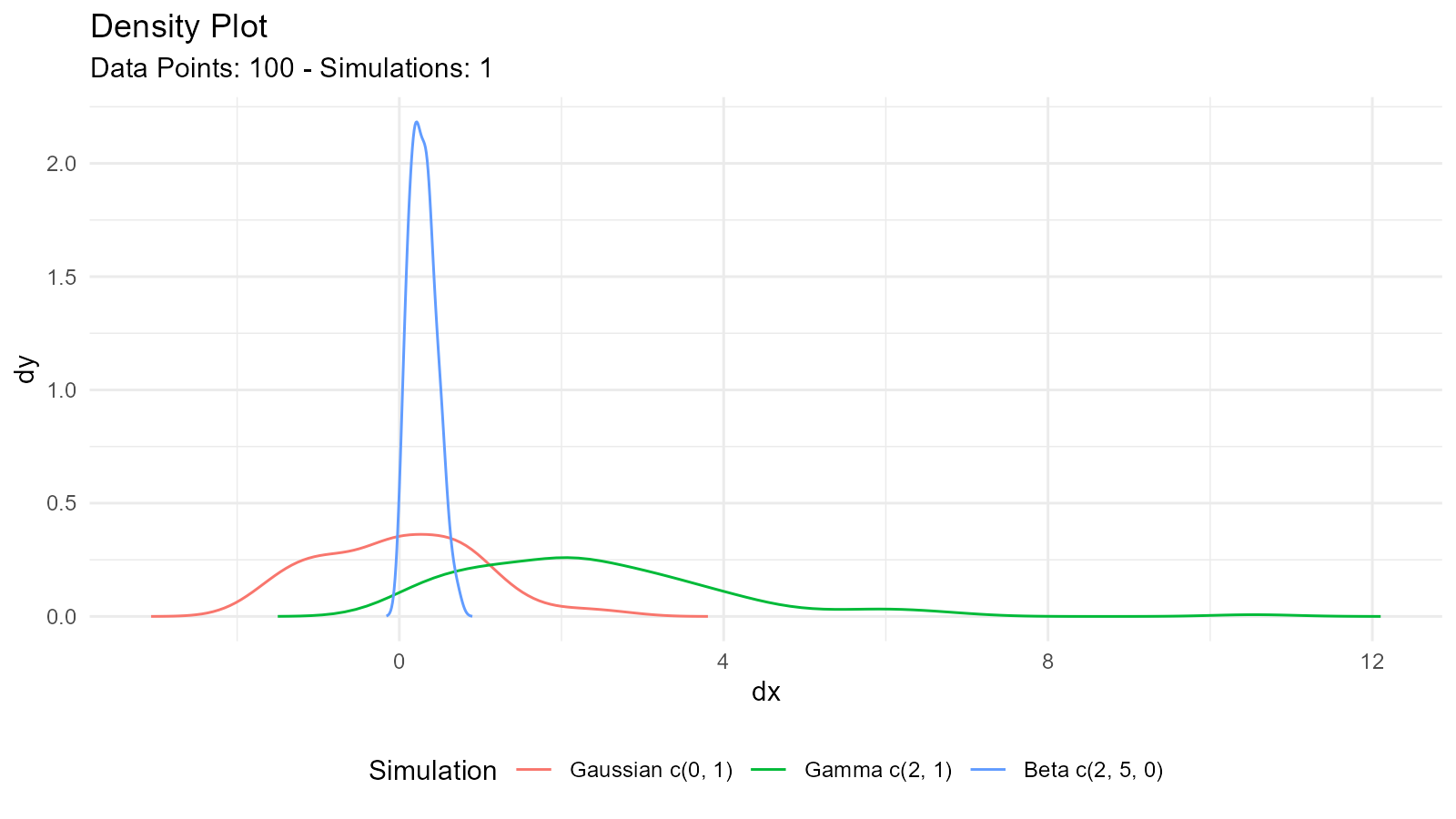

Combined density plot showing normal, gamma, and beta distributions overlaid, allowing comparison of their different shapes and support ranges

Multi-Single Distribution Table

Create comparison table for same distribution with varying parameters:

# Generate multiple parameter sets
multi_beta <- tidy_multi_single_dist(
  .tidy_dist = "tidy_beta",
  .param_list = list(
    .n = 100,
    .shape1 = c(1, 2, 5, 5),
    .shape2 = c(1, 5, 2, 5),
    .ncp = 0,
    .num_sims = 1,
    .return_tibble = TRUE
  )
)

# Visualize
tidy_multi_dist_autoplot(multi_beta)

Density plot comparing four beta distributions with different shape parameters, showing how shape1 and shape2 affect the distribution shape from uniform to highly skewed

Quantile Normalization

What is Quantile Normalization?

Transform data to have a specific distribution while preserving ranks:

# Your data
data_mat <- matrix(c(5, 2, 8, 3, 9, 1, 7, 4, 6), 3, 3)

# Normalize to range [0, 1]
normalized <- quantile_normalize(data.frame(data_mat))

# Compare original and normalized
cat("Original Data: \n")
#> Original Data:
print(data_mat)
#>      [,1] [,2] [,3]
#> [1,]    5    3    7
#> [2,]    2    9    4
#> [3,]    8    1    6
cat("\n")

cat("Normalized Data: \n")
#> Normalized Data:
print(normalized)
#>            X1       X2       X3
#> [1,] 4.666667 4.666667 8.000000
#> [2,] 2.333333 8.000000 2.333333
#> [3,] 8.000000 2.333333 4.666667
cat("\n")

Advanced Plotting

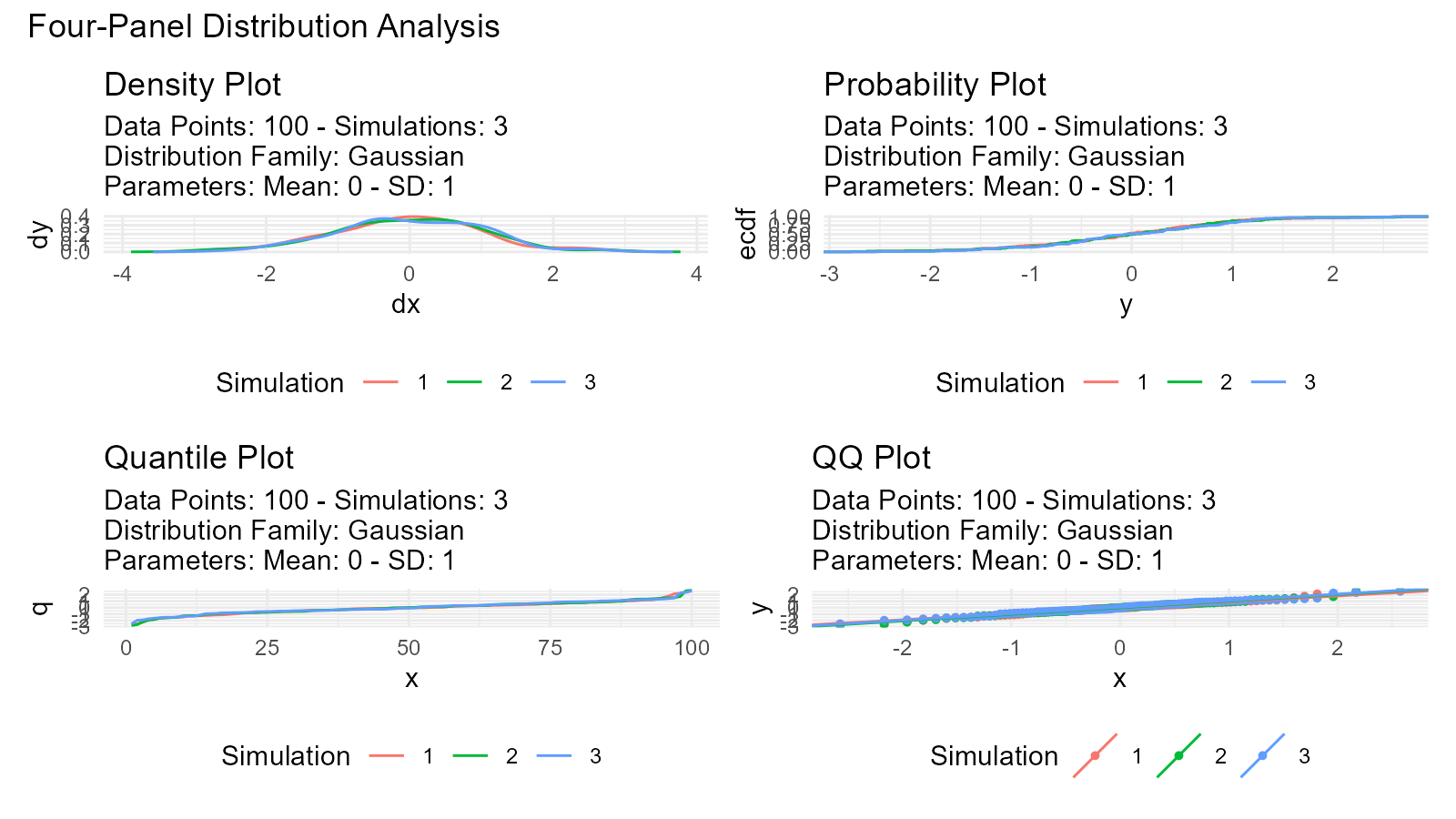
Four-Panel Plots

View multiple plot types simultaneously:

data <- tidy_normal(.n = 100, .num_sims = 3)

# Create all plot types
p1 <- tidy_autoplot(data, .plot_type = "density")
p2 <- tidy_autoplot(data, .plot_type = "probability")
p3 <- tidy_autoplot(data, .plot_type = "quantile")
p4 <- tidy_autoplot(data, .plot_type = "qq")

# Combine in 2x2 grid
(p1 | p2) / (p3 | p4) +
  plot_annotation(
    title = "Four-Panel Distribution Analysis"
  )

Four-panel display showing density, probability, quantile, and Q-Q plots for normal distribution simulations, providing a comprehensive view of the distribution characteristics

Triangular Distribution Plots 

# Triangular distribution
tri <- tidy_triangular(
  .n = 100,
  .min = 0,
  .max = 10,
  .mode = 7
)

# Visualize
tidy_autoplot(tri, .plot_type = "density")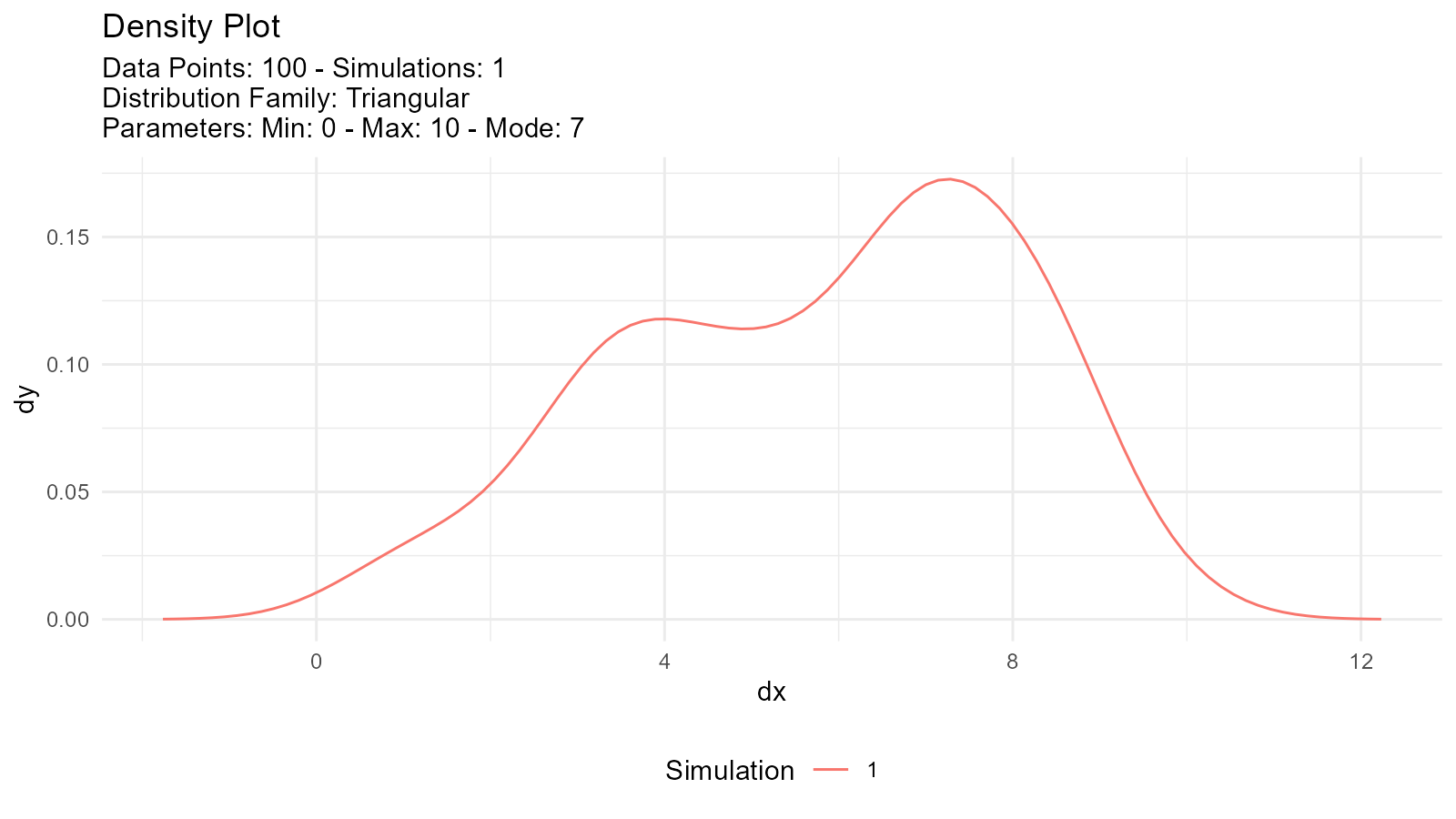

Density plot of a triangular distribution with minimum 0, maximum 10, and mode 7, showing the characteristic triangular shape

Real-World Examples

Example 1: Modeling Bimodal Data 

# Simulate bimodal data (two age groups)
young <- tidy_normal(.n = 200, .mean = 25, .sd = 3)
old <- tidy_normal(.n = 150, .mean = 65, .sd = 5)

# Create mixture model
age_distribution <- tidy_mixture_density(
  young, old,
  .combination_type = "stack"
)

age_distribution$plots
#> $line_plot

Density plot of a bimodal age distribution modeling two population groups: young adults centered at 25 years and older adults centered at 65 years

#> 
#> $dens_plot

Density plot of a bimodal age distribution modeling two population groups: young adults centered at 25 years and older adults centered at 65 years

Example 2: Quality Control 

# Good products (tight distribution)
# Defective products (wider distribution)
good <- tidy_normal(.n = 95, .mean = 100, .sd = 2)
defective <- tidy_normal(.n = 5, .mean = 100, .sd = 10)

# Mixture model
qc_distribution <- tidy_mixture_density(
  good, defective,
  .combination_type = "stack"
)

qc_distribution$plots
#> $line_plot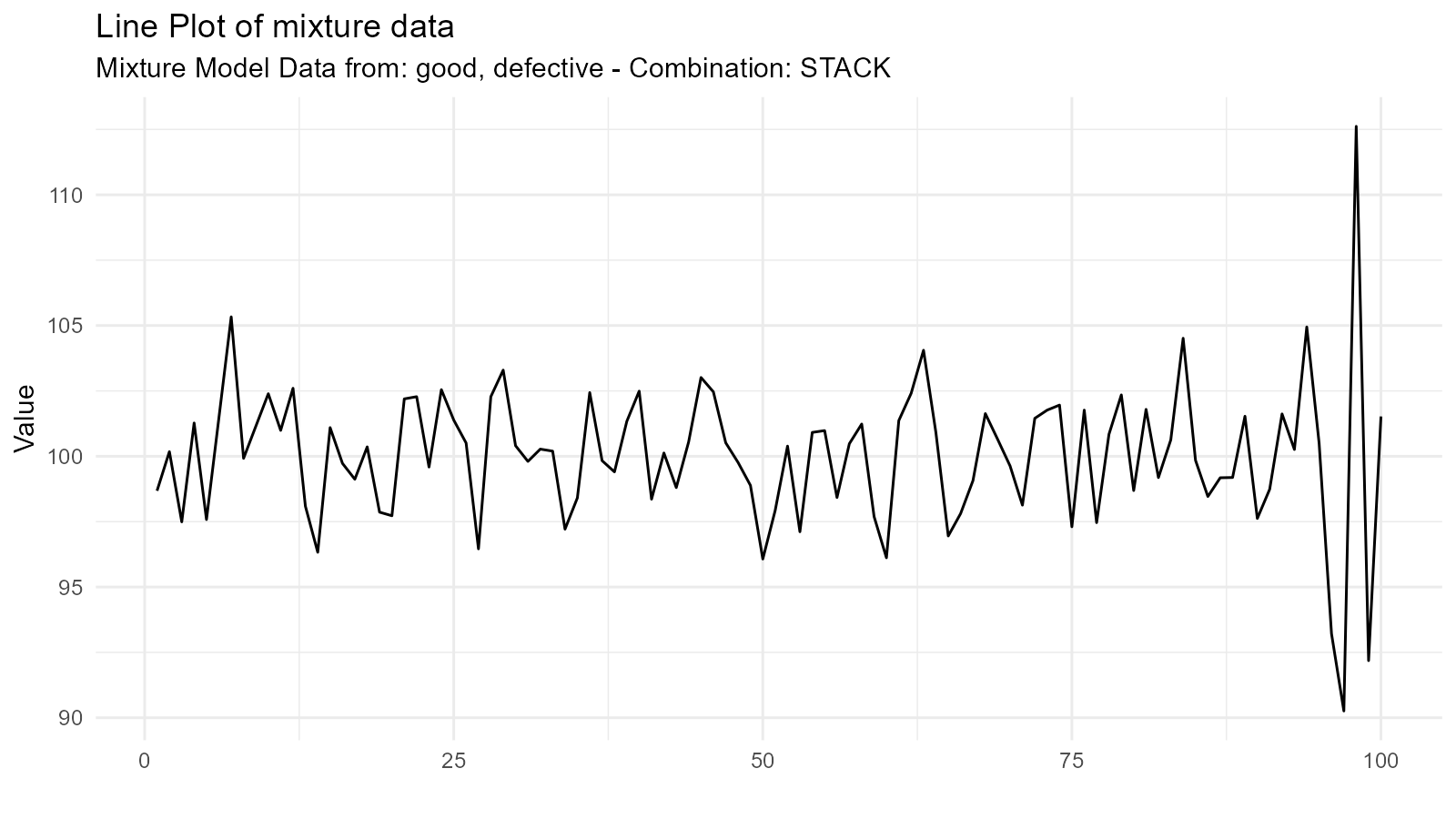

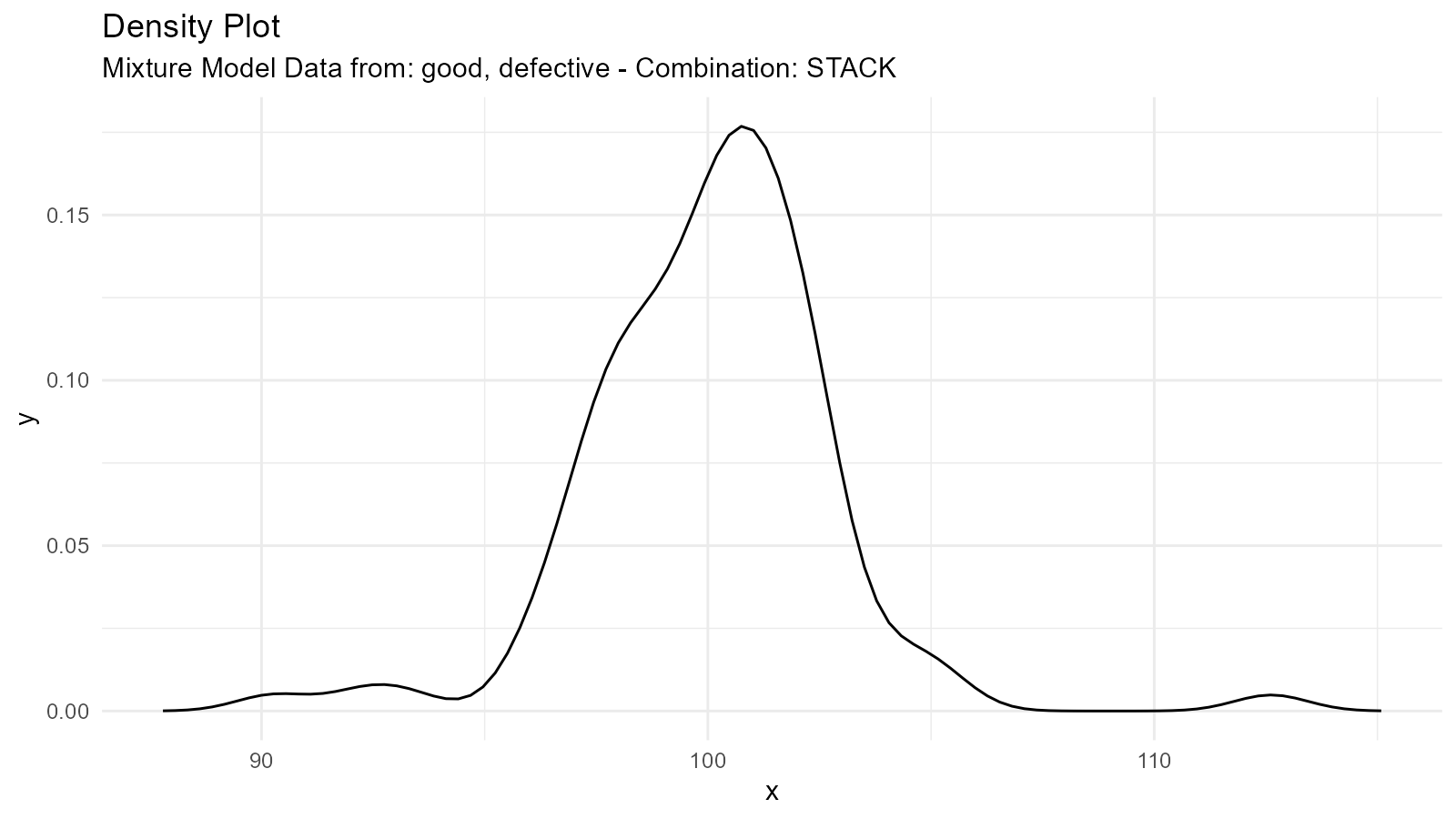
Density plot of a quality control distribution showing a tight peak for good products (95%) and a wider spread for defective products (5%)

#> 
#> $dens_plot

Density plot of a quality control distribution showing a tight peak for good products (95%) and a wider spread for defective products (5%)

Tips and Tricks

Tip 1: Validate Mixture Models 

# Create mixture
mixture <- tidy_mixture_density(
  rnorm(50, -2, 1), rnorm(50, 2, 1),
  .combination_type = "stack"
)

# Extract key statistics from the mixture density data
mixture_stats <- mixture$data$dens_tbl |>
  dplyr::summarise(
    mean_x = mean(x, na.rm = TRUE),
    sd_x = sd(x, na.rm = TRUE),
    median_x = median(x, na.rm = TRUE)
  )

mixture_stats
#> # A tibble: 1 × 3
#>   mean_x  sd_x median_x
#>    <dbl> <dbl>    <dbl>
#> 1  0.134  4.19    0.134

Tip 2: Debug by Plotting Components Separately

If a mixture doesn’t look right, plot the components individually:

# Debug by plotting components separately
dist1 <- tidy_normal(.mean = -2)
dist2 <- tidy_normal(.mean = 2)
p1 <- tidy_autoplot(dist1, .plot_type = "density") +
  ggtitle("Component 1")
p2 <- tidy_autoplot(dist2, .plot_type = "density") +
  ggtitle("Component 2")

p1 | p2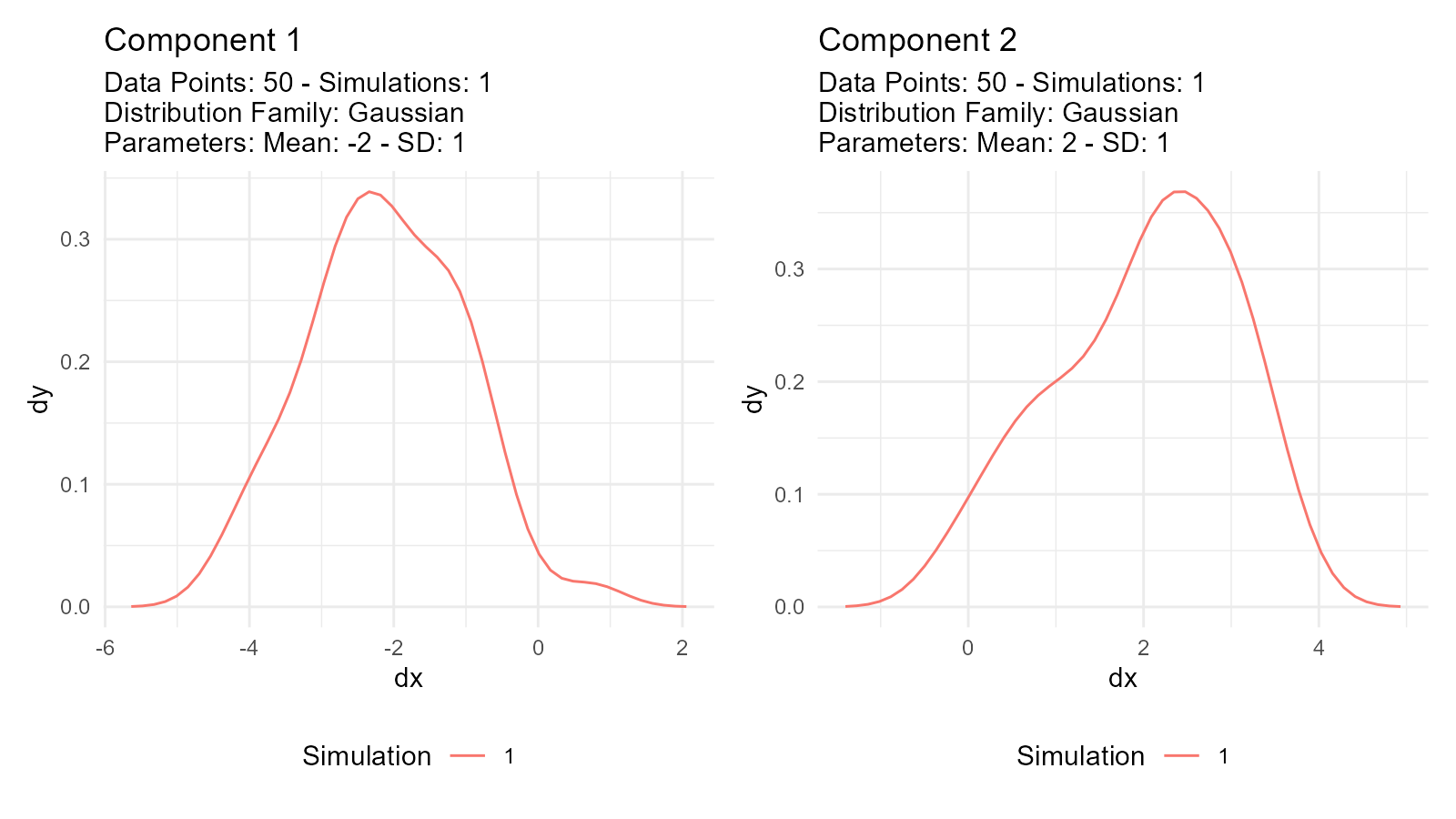

Two density plots showing the individual component distributions before mixing, useful for debugging mixture models

Troubleshooting

Issue: Mixture Doesn’t Look Right

Check:

  • Are component distributions on appropriate scales?
  • Are mixture weights (via .n) appropriate?
  • Is the mixture type correct?

Issue: Empirical Distribution Too Noisy

Solution: Use multiple simulations for smoothing:

# Increase sample size via resampling
empirical_smooth <- tidy_empirical(.x = mtcars$mpg, .num_sims = 10)
tidy_autoplot(empirical_smooth, .plot_type = "density")

Density plot showing 10 bootstrap resamples of empirical data, demonstrating how multiple simulations can smooth the estimated distribution

Issue: Multi-Distribution Plots Cluttered

Solution: Reduce the number of comparisons or use interactive plots.